题目内容
选修 4- 5 :不等式选讲
设函数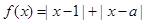 ,
,
(1)若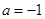 ,解不等式
,解不等式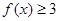 ;(2)如果
;(2)如果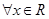 ,
,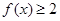 ,求a的取值范围。
,求a的取值范围。
设函数
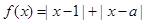 ,
,(1)若
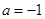 ,解不等式
,解不等式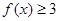 ;(2)如果
;(2)如果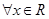 ,
,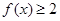 ,求a的取值范围。
,求a的取值范围。(1) (2)
(2)
 (2)
(2)
本试题主要是考查了绝对值不等式的求解和不等式恒成立的求解参数 范围问题。
(1)当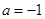 时,
时, ,由
,由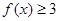 得:
得:
(2)对于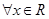 ,
,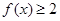 的充要条件是
的充要条件是 ,然后求解函数的最小值得到结论。
,然后求解函数的最小值得到结论。
解:(1)当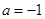 时,
时, ,由
,由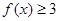 得:
得: ,
,
(法一)由绝对值的几何意义知不等式的解集为 。
。
(法二)不等式可化为 或
或 或
或 ,
,
∴不等式的解集为 。-------------5分
。-------------5分
(2)若 ,
, ,不满足题设条件;
,不满足题设条件;
若 ,
, ,
, 的最小值为
的最小值为 ;
;
若 ,
, ,
, 的最小值为
的最小值为 。
。
所以对于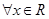 ,
,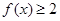 的充要条件是
的充要条件是 ,从而a的取值范围
,从而a的取值范围 。-------------10分
。-------------10分
(1)当
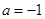 时,
时, ,由
,由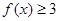 得:
得:
(2)对于
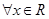 ,
,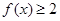 的充要条件是
的充要条件是 ,然后求解函数的最小值得到结论。
,然后求解函数的最小值得到结论。解:(1)当
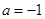 时,
时, ,由
,由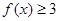 得:
得: ,
,(法一)由绝对值的几何意义知不等式的解集为
 。
。(法二)不等式可化为
 或
或 或
或 ,
,∴不等式的解集为
 。-------------5分
。-------------5分(2)若
 ,
, ,不满足题设条件;
,不满足题设条件;若
 ,
, ,
, 的最小值为
的最小值为 ;
;若
 ,
, ,
, 的最小值为
的最小值为 。
。所以对于
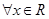 ,
,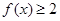 的充要条件是
的充要条件是 ,从而a的取值范围
,从而a的取值范围 。-------------10分
。-------------10分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的解集为_____.
的解集为_____.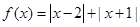
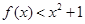 ;
;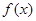 ≤
≤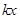 的解集为空集,求
的解集为空集,求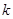 的取值范围。
的取值范围。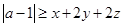 ,对满足
,对满足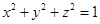 的一切实数
的一切实数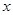 、
、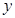 、
、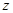 恒成立,则实数a的取值范围 .
恒成立,则实数a的取值范围 .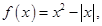 若
若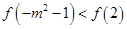 ,则实数
,则实数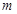 的取值范围
的取值范围 的最小值.
的最小值. 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围. 的解集
的解集  >2的解集为 .
>2的解集为 .