题目内容
先解答（Ⅰ），再通过结构类比解答（Ⅱ）：
（Ⅰ）求证：tan(x+
)=
；
（Ⅱ） 设x∈R且f（x+π）=
，试问：f（x）是周期函数吗？证明你的结论．
（Ⅰ）求证：tan(x+
| π |
| 4 |
| 1+tanx |
| 1-tanx |
（Ⅱ） 设x∈R且f（x+π）=
| 1+f(x) |
| 1-f(x) |
（Ⅰ）证明：tan(x+
)=
=
．
（Ⅱ）f（x）是以4π为其一个周期的周期函数．
f(x+2π)=f(x+π+π)=
=
=-
，
∴f(x+4π)=f[(x+2π)+2π]=-
=-
=f(x)，
所以f（x）是周期函数，其中一个周期为4π．
| π |
| 4 |
tanx+tan
| ||
1-tanxtan
|
| 1+tanx |
| 1-tanx |
（Ⅱ）f（x）是以4π为其一个周期的周期函数．
f(x+2π)=f(x+π+π)=
| 1+f(x+π) |
| 1-f(x+π) |
1+
| ||
1-
|
| 1 |
| f(x) |
∴f(x+4π)=f[(x+2π)+2π]=-
| 1 |
| f(x+2π) |
| 1 | ||
-
|
所以f（x）是周期函数，其中一个周期为4π．
练习册系列答案
相关题目
，并写出函数
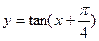的最小正周期；
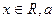为非零常数，且
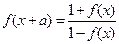，试问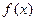
是周期函数吗？证明你的结论。
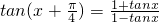；②用反证法证明：函数f（x）=tanx的最小正周期是π；
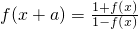，试问：f（x）是周期函数吗？证明你的结论．
；
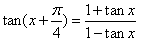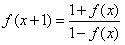，试问：f(x)是周期函数吗？证明你的结论。