题目内容
设函数f(x)=x(x-1)(x-a),(a>1)。
(1)求导数f′(x),并证明f(x)有两个不同的极值点x1,x2;
(2)若不等式f(x1)+f(x2)≤0成立,求a的取值范围。
(1)求导数f′(x),并证明f(x)有两个不同的极值点x1,x2;
(2)若不等式f(x1)+f(x2)≤0成立,求a的取值范围。
解: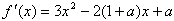
令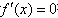 得方程
得方程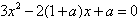
因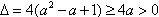
故方程有两个不同实根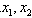
不妨设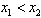
由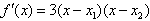 可判定f′(x)的符号如下:
可判定f′(x)的符号如下:
当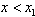 时,f'(x)>0
时,f'(x)>0
当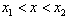 时,
时,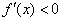
当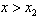 时,
时,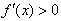
因此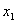 是极大值点,
是极大值点,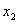 是极小值点。
是极小值点。
(2)因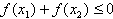 ,故得不等式
,故得不等式
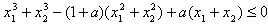
即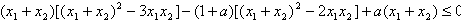
又由(1)知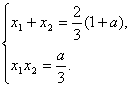
代入前面不等式,两边除以(1+a),并化简得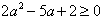
解不等式得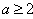 或
或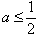 (舍去)
(舍去)
因此,当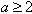 时,不等式
时,不等式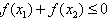 成立。
成立。
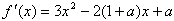
令
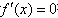 得方程
得方程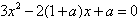
因
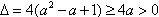
故方程有两个不同实根
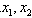
不妨设
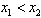
由
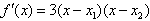 可判定f′(x)的符号如下:
可判定f′(x)的符号如下:当
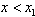 时,f'(x)>0
时,f'(x)>0当
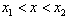 时,
时,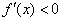
当
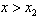 时,
时,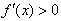
因此
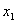 是极大值点,
是极大值点,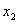 是极小值点。
是极小值点。(2)因
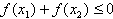 ,故得不等式
,故得不等式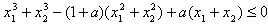
即
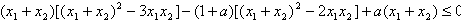
又由(1)知
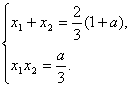
代入前面不等式,两边除以(1+a),并化简得
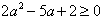
解不等式得
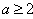 或
或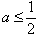 (舍去)
(舍去)因此,当
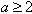 时,不等式
时,不等式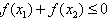 成立。
成立。
练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
设函数f(x)的定义域为A,若存在非零实数t,使得对于任意x∈C(C⊆A),有x+t∈A,且f(x+t)≤f(x),则称f(x)为C上的t低调函数.如果定义域为[0,+∞)的函数f(x)=-|x-m2|+m2,且 f(x)为[0,+∞)上的10低调函数,那么实数m的取值范围是( )
| A、[-5,5] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|