Question

求证：．.

 

Answer 1

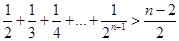
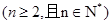【答案】

运用数学归纳法来证明关于与自然数相关的不等式的命题，分为两步来证明即可。

【解析】

试题分析：证明　①当n＝2时，左＝>0＝右，∴不等式成立．

②假设当n＝k(k≥2，k∈N^*)时，不等式成立．

即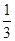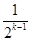＋＋…＋>成立．

那么n＝k＋1时，＋＋…＋＋＋…＋

>＋＋…＋>＋＋＋…＋

＝＋＝，

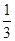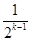∴当n＝k＋1时，不等式成立．

据①②可知，不等式对一切n∈N^*且n≥2时成立．

考点：数学归纳法

点评：主要是考查了运用数学归纳法来证明与自然数相关的命题的运用，属于基础题。