题目内容
已知二项式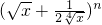 的展开式中,前三项的系数成等差数列.
的展开式中,前三项的系数成等差数列.
(1)求n;
(2)求展开式中的一次项;
(3)求展开式中所有项的二项式系数之和.
解:(1)前三项的系数为 ,…(1分)
,…(1分)
由题设,得 ,…(2分)
,…(2分)
即n2-9n+8=0,解得n=8或n=1(舍去). …(4分)
(2) =
= ,…(6分)
,…(6分)
令 ,得r=4.…(8分)
,得r=4.…(8分)
所以展开式中的一次项为 .…(10分)
.…(10分)
(3)∵C80+C81+C82+…+C88=28=256,
∴所有项的二项式系数和为256.…(14分)
分析:(1)由题意二项式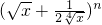 的展开式中,前三项的系数成等差数列,可得出
的展开式中,前三项的系数成等差数列,可得出 ,解此方程求出n的值;
,解此方程求出n的值;
(2)由项的展开式 整理得
整理得 ,令x的指数为1,解出r的值,即可求得一次项;
,令x的指数为1,解出r的值,即可求得一次项;
(3)二项式系数的和为C80+C81+C82+…+C88的和,计算出它的值即得.
点评:本题考点二项式系数的性质,考查了二项式的项,等差数列的性质,二项式系数和的公式,解题的关键是熟练掌握二项式的性质及等差数列的性质,二项式的性质是一个非常重要的考点,也是每年高考的必考点,本题很典型,包括了二项式的主要性质,题后注意总结
 ,…(1分)
,…(1分)由题设,得
 ,…(2分)
,…(2分)即n2-9n+8=0,解得n=8或n=1(舍去). …(4分)
(2)
 =
= ,…(6分)
,…(6分)令
 ,得r=4.…(8分)
,得r=4.…(8分)所以展开式中的一次项为
 .…(10分)
.…(10分)(3)∵C80+C81+C82+…+C88=28=256,
∴所有项的二项式系数和为256.…(14分)
分析:(1)由题意二项式
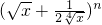 的展开式中,前三项的系数成等差数列,可得出
的展开式中,前三项的系数成等差数列,可得出 ,解此方程求出n的值;
,解此方程求出n的值;(2)由项的展开式
 整理得
整理得 ,令x的指数为1,解出r的值,即可求得一次项;
,令x的指数为1,解出r的值,即可求得一次项;(3)二项式系数的和为C80+C81+C82+…+C88的和,计算出它的值即得.
点评:本题考点二项式系数的性质,考查了二项式的项,等差数列的性质,二项式系数和的公式,解题的关键是熟练掌握二项式的性质及等差数列的性质,二项式的性质是一个非常重要的考点,也是每年高考的必考点,本题很典型,包括了二项式的主要性质,题后注意总结

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知二项式 的展开式中第4项为常数项,则
的展开式中第4项为常数项,则 项的系数为 ( )
项的系数为 ( )
| A.-19 | B.19 | C.20 | D.-20 |
 的展开式中第4项为常数项,则
的展开式中第4项为常数项,则 项的系数为( )
项的系数为( ) 的展开式中,各项系数的和与其各项二项式系数的和之比为64,则展开式中
的展开式中,各项系数的和与其各项二项式系数的和之比为64,则展开式中 的系数等于__
__ .
的系数等于__
__ . 的展开式中各项系数和为64.
的展开式中各项系数和为64. ;
;  的展开式中第4项为常数项,则
的展开式中第4项为常数项,则 项的系数为 ( )
项的系数为 ( )