题目内容
设等比数列{an}的公比为q,前n项和Sn>0(n=1,2,…).(1)求q的取值范围;
(2)设bn=an+2-![]() an+1,记{bn}的前n项和为Tn,试比较Sn与Tn的大小.
an+1,记{bn}的前n项和为Tn,试比较Sn与Tn的大小.
解:(1)因为{an}是等比数列,Sn>0,可得a1=S1>0,q≠0.
当q=1时,Sn=na1>0;
当q≠1时,Sn=![]() >0,即
>0,即![]() >0.
>0.
上式等价于不等式组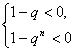 ①
①
或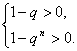 ②
②
解①得q>1;
解②得-1<q<0或0<q<1.
综上,q的取值范围是(-1,0)∪(0,+∞).
(2)由bn=an+2-![]() an+1,得
an+1,得
bn=an(q2-![]() q),Tn=(q2-
q),Tn=(q2-![]() q)Sn.
q)Sn.
于是Tn-Sn=Sn(q2-![]() q-1)=Sn(q+
q-1)=Sn(q+![]() )(q-2).
)(q-2).
又因为Sn>0且-1<q<0或q>0,所以,
当-1<q<-![]() 或q>2时,Tn-Sn>0,即Tn>Sn;
或q>2时,Tn-Sn>0,即Tn>Sn;
当-![]() <q<2且q≠0时,Tn-Sn<0,即Tn<Sn;
<q<2且q≠0时,Tn-Sn<0,即Tn<Sn;
当q=-![]() 或q=2时,Tn-Sn=0,即Tn=Sn.
或q=2时,Tn-Sn=0,即Tn=Sn.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
设等比数列{an}的前n项和为Sn,若8a2+a5=0,则下列式子中数值不能确定的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设等比数列{an}的前n项和为Sn,若
=3,则
=( )
| S6 |
| S3 |
| S9 |
| S6 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |