题目内容
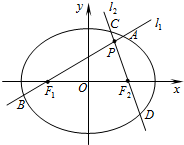 中心在坐标原点,焦点在x轴上的椭圆的离心率为
中心在坐标原点,焦点在x轴上的椭圆的离心率为
| ||
| 3 |
2
| ||
| 3 |
(1)求椭圆的方程;
(2)是否存在定点M、N,使得|PM|+|PN|为定值.若存在,求出M、N点坐标;若不存在,说明理由.
分析:(1)设椭圆方程为
+
=1(a>b>0),则由题意
解得即可;
(2)当直线l1或l2斜率不存在时,P点坐标为(-1,0)或(1,0).当直线l1、l2斜率存在时,设斜率分别为m1,m2.可得l1的方程为y=m1(x+1),l2的方程为y=m2(x-1).设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),与椭圆方程联立即可得出根与系数的关系,再利用斜率计算公式和已知即可得出m1与m2的关系,进而得出答案.
| x2 |
| a2 |
| y2 |
| b2 |
|
(2)当直线l1或l2斜率不存在时,P点坐标为(-1,0)或(1,0).当直线l1、l2斜率存在时,设斜率分别为m1,m2.可得l1的方程为y=m1(x+1),l2的方程为y=m2(x-1).设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),与椭圆方程联立即可得出根与系数的关系,再利用斜率计算公式和已知即可得出m1与m2的关系,进而得出答案.
解答:解:(1)设椭圆方程为
+
=1(a>b>0),
则由题意
解得
∴椭圆方程为
+
=1.
(2)当直线l1或l2斜率不存在时,P点坐标为(-1,0)或(1,0).
当直线l1、l2斜率存在时,设斜率分别为m1,m2.
∴l1的方程为y=m1(x+1),l2的方程为y=m2(x-1).
设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
联立
,得到(2+3
)x2+6
x+3
-6=0,
∴x1+x2=-
,x1x2=
.
同理x3+x4=
,x3x4=
.(*)
∵k1=
=
=m1+
,k2=m1+
,k3=m2-
,k4=m2-
.
又满足k1+k2=k3+k4.
∴2m1+m1•
=2m2-m2•
,
把(*)代入上式化为:2m1+m1•
=2m2-m2•
.(m1≠m2).
化为m1m2=-2.
设点P(x,y),则
•
=-2,(x≠±1)
化为
+x2=1.
由当直线l1或l2斜率不存在时,P点坐标为(-1,0)或(1,0)也满足,
∴点P在椭圆上,则存在点M、N其坐标分别为(0,-1)、(0,1),使得|PM|+|PN|=2
为定值.
| x2 |
| a2 |
| y2 |
| b2 |
则由题意
|
|
∴椭圆方程为
| x2 |
| 3 |
| y2 |
| 2 |
(2)当直线l1或l2斜率不存在时,P点坐标为(-1,0)或(1,0).
当直线l1、l2斜率存在时,设斜率分别为m1,m2.
∴l1的方程为y=m1(x+1),l2的方程为y=m2(x-1).
设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
联立
|
| m | 2 1 |
| m | 2 1 |
| m | 2 1 |
∴x1+x2=-
6
| ||
2+3
|
3
| ||
2+3
|
同理x3+x4=
6
| ||
2+3
|
3
| ||
2+3
|
∵k1=
| y1 |
| x1 |
| m1(x1+1) |
| x1 |
| m1 |
| x1 |
| m1 |
| x2 |
| m2 |
| x3 |
| m2 |
| x4 |
又满足k1+k2=k3+k4.
∴2m1+m1•
| x1+x2 |
| x1x2 |
| x3+x4 |
| x3x4 |
把(*)代入上式化为:2m1+m1•
-2
| ||
|
2
| ||
|
化为m1m2=-2.
设点P(x,y),则
| y |
| x+1 |
| y |
| x-1 |
化为
| y2 |
| 2 |
由当直线l1或l2斜率不存在时,P点坐标为(-1,0)或(1,0)也满足,
∴点P在椭圆上,则存在点M、N其坐标分别为(0,-1)、(0,1),使得|PM|+|PN|=2
| 2 |
点评:熟练掌握椭圆的定义、标准方程及其性质、直线与椭圆相交问题转化为方程联立可得出根与系数的关系、斜率计算公式等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
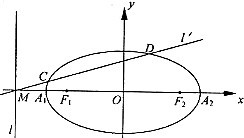 已知椭圆的中心在坐标原点,焦点F1、F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,
已知椭圆的中心在坐标原点,焦点F1、F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M, (2011•延庆县一模)已知椭圆C的中心在坐标原点,焦点在x轴上,它的一个顶点B与抛物线x2=4y的焦点重合,离心率
(2011•延庆县一模)已知椭圆C的中心在坐标原点,焦点在x轴上,它的一个顶点B与抛物线x2=4y的焦点重合,离心率