Question

【题目】现有半径为R、圆心角（∠AOB）为90°的扇形材料，要裁剪出一个五边形工件OECDF，如图所示．其中E，F分别在OA，OB上，C，D在 上，且OE=OF，EC=FD，∠ECD=∠CDF=90°．记∠COD=2θ，五边形OECDF的面积为S．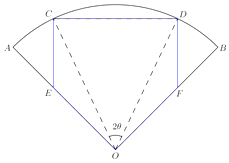
（1）试求S关于θ的函数关系式；
（2）求S的最大值．

Answer 1

【答案】
（1）解：设M是CD中点，连OM，由OC=OD，可知OM⊥CD，

∠COM=∠DOM=， ，MD=Rsinθ，

又OE=OF，EC=FD，OC=OD，可得△CEO≌△DFO，

故∠EOC=∠DOF，可知 ，

又DF⊥CD，OM⊥CD，所以MO∥DF，故∠DFO= ，

在△DFO中，有 ，

可得

所以S=S△COD+SODF+SOCE=S△COD+2SODF=

=

（2）解：

= （其中 ）

当 ，即 时，sin（2θ+φ）取最大值1．

又 ，所以S的最大值为 ．

【解析】（1）设M是CD中点，连OM，推出∠COM=∠DOM= ，MD=Rsinθ，利用△CEO≌△DFO，转化求解∠DFO= ，在△DFO中，利用正弦定理 ，求解S=S△COD+SODF+SOCE=S△COD+2SODF的解析式即可．（2）利用S的解析式，通过三角函数的最值求解即可．