题目内容
设A(x1,y1),B(x2,y2)是函数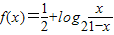 的图象上任意两点,且
的图象上任意两点,且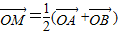 ,已知M的横坐标为
,已知M的横坐标为 .
.(1)求证:M点的纵坐标为定值;
(2)若
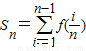 ,其中n∈N*,且n≥2,求Sn;
,其中n∈N*,且n≥2,求Sn;(3)已知
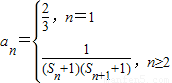 ,其中n∈N*,Tn为数列{an}的前n项和,Tn<λ(Sn+1+1),对一切n∈N*都成立,试求λ的取值范围.
,其中n∈N*,Tn为数列{an}的前n项和,Tn<λ(Sn+1+1),对一切n∈N*都成立,试求λ的取值范围.
【答案】分析:(1)由题设条件知M是AB的中点,由中点坐标公式可以求出M点的给坐标.
(2)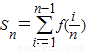 =
=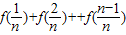 ,即
,即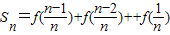
以上两式相加后两边再同时除以2就得到Sn.
(3)当n≥2时,根据题设条件,由Tn<λ(Sn+1+1)得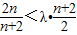 ,
,
∴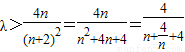 ,再由均值不等式求出λ的取值范围.
,再由均值不等式求出λ的取值范围.
解答:解:(1)∵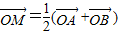
∴M是AB的中点,设M点的坐标为M(x,y),
由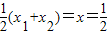 ,得x1+x2=1,则x2=1-x1
,得x1+x2=1,则x2=1-x1
而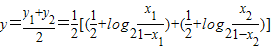
=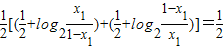
∴M点的纵坐标为定值
(2)由(1)知若x1+x2=1则f(x1)+f(x2)=y1+y2=1,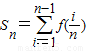 =
=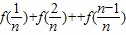
即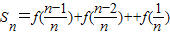
以上两式相加得: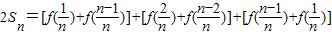 ═
═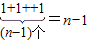
∴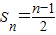
(3)当n≥2时,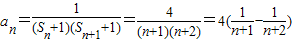
∴Tn=a1+a2+…+an=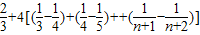 =
=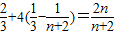
由Tn<λ(Sn+1+1)得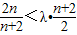
∴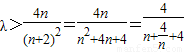
∵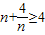 ,当且仅当n=2时“=”成立
,当且仅当n=2时“=”成立
∴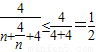 .
.
因此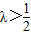 ,即λ的取值范围为
,即λ的取值范围为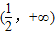
点评:本题考查了中点坐标公式、数列求和、均值不等式、对数性质等知识点,难说度较大,解题时要认真审题,仔细作答.
(2)
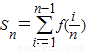 =
=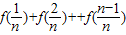 ,即
,即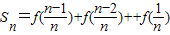
以上两式相加后两边再同时除以2就得到Sn.
(3)当n≥2时,根据题设条件,由Tn<λ(Sn+1+1)得
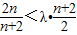 ,
,∴
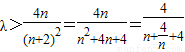 ,再由均值不等式求出λ的取值范围.
,再由均值不等式求出λ的取值范围.解答:解:(1)∵
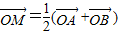
∴M是AB的中点,设M点的坐标为M(x,y),
由
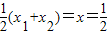 ,得x1+x2=1,则x2=1-x1
,得x1+x2=1,则x2=1-x1而
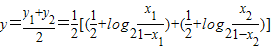
=
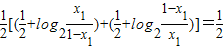
∴M点的纵坐标为定值

(2)由(1)知若x1+x2=1则f(x1)+f(x2)=y1+y2=1,
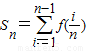 =
=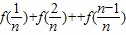
即
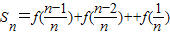
以上两式相加得:
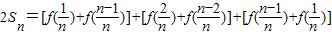 ═
═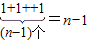
∴
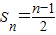
(3)当n≥2时,
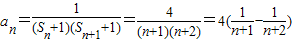
∴Tn=a1+a2+…+an=
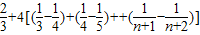 =
=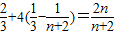
由Tn<λ(Sn+1+1)得
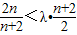
∴
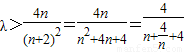
∵
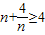 ,当且仅当n=2时“=”成立
,当且仅当n=2时“=”成立∴
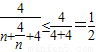 .
.因此
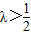 ,即λ的取值范围为
,即λ的取值范围为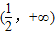
点评:本题考查了中点坐标公式、数列求和、均值不等式、对数性质等知识点,难说度较大,解题时要认真审题,仔细作答.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
