题目内容
已知函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若直线 与函数
与函数 的图像有
的图像有 个交点,求
个交点,求 的取值范围.
的取值范围.
【答案】
(1)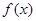 的增区间是
的增区间是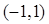 ,
,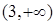 ;减区间是
;减区间是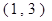
(2)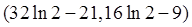
【解析】本试题主要是考查了导数在研究函数中的运用,求解函数的单调区间和函数与函数图像的交点问题的综合运用。
(1)因为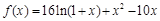 ,
,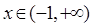
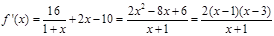
从而得到单调增减区间。
(2)要使直线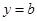 与函数
与函数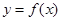 的图像有
的图像有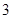 个交点,则可以由(1)知,
个交点,则可以由(1)知, 在
在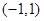 上单调递增,在
上单调递增,在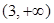 上单调递增,在
上单调递增,在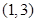 上单调递减.∴
上单调递减.∴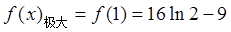 ,
,
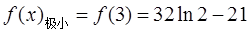
根据极值的正负来得到参数的范围。
解(1)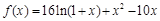 ,
,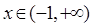
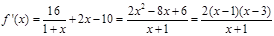 …………………3分
…………………3分
令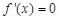 ,得
,得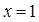 ,
,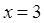 …………………5分
…………………5分
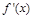 和
和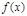 随
随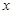 的变化情况如下:
的变化情况如下:
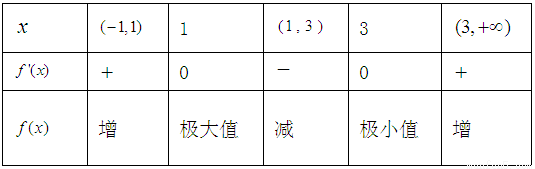
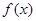 的增区间是
的增区间是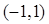 ,
,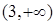 ;减区间是
;减区间是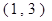 …………………8分
…………………8分
(2)由(1)知, 在
在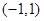 上单调递增,在
上单调递增,在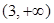 上单调递增,在
上单调递增,在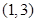 上单调递减.
上单调递减.
∴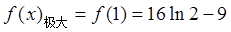 ,
,
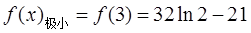 …………………10分
…………………10分
又 时,
时,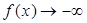 ;
;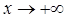 时,
时,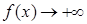 ;
;
可据此画出函数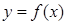 的草图(图1),由图可知,
的草图(图1),由图可知,
当直线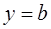 与函数
与函数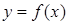 的图像有3个交点时,
的图像有3个交点时, 的取值范围为
的取值范围为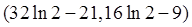 …………………13分
…………………13分

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 .
. 的定义域
;
的定义域
; ,求实数
,求实数 的值.
的值. .
. 在(0,+∞)上是减函数.
在(0,+∞)上是减函数.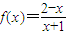 ;
; 成立,若存在求出x;若不存在,请说明理由.
成立,若存在求出x;若不存在,请说明理由. 令
令
 的定义域;
的定义域; 的奇偶性,并予以证明;
的奇偶性,并予以证明; ,猜想
,猜想 之间的关系并证明.
之间的关系并证明. ,
, 的定义域;(2)证明:
的定义域;(2)证明: ,求
,求 的取值范围。
的取值范围。