题目内容
(文)如图,已知双曲线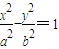 ,F1,F2分别是它的左、右焦点,P2P⊥F1F2,交双曲线于P点,连接F1P交双曲线于另一点Q,分别与双曲线的渐近线交于A,B,且∠F1PF2=60°.
,F1,F2分别是它的左、右焦点,P2P⊥F1F2,交双曲线于P点,连接F1P交双曲线于另一点Q,分别与双曲线的渐近线交于A,B,且∠F1PF2=60°.(1)求双曲线的离心率;(2)求
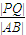 的值.
的值.
【答案】分析:(1)△F1F2P中,|F1F2|=2c∠F1PF2=60°,故 ,由此能求出双曲线的离心率.
,由此能求出双曲线的离心率.
(2)由e= ,知b2=2a2,设双曲线方程为
,知b2=2a2,设双曲线方程为 ,直线PF1:
,直线PF1: ,则
,则 ,由此能求出
,由此能求出 的值.
的值.
解答:解:(1)△F1F2P中,|F1F2|=2c∠F1PF2=60°
∴ …(2分)
…(2分)
∴ ,
,
∴ …(5分)
…(5分)
(2)∵ ,
,
∴b2=2a2,
设双曲线方程为 ,
,
即2x2-y2=2a2,①…(7分)
直线PF1: ,
,
即 ,②…(8分)
,②…(8分)
由①②得
∴ …(11分)
…(11分)
再由双曲线的渐进线方程2x2-y2=0,
∴|AB|= ,
,
∴ .…(13分)
.…(13分)
点评:题主要考查双曲线标准方程,简单几何性质,直线与双曲线的位置关系等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.
 ,由此能求出双曲线的离心率.
,由此能求出双曲线的离心率.(2)由e=
 ,知b2=2a2,设双曲线方程为
,知b2=2a2,设双曲线方程为 ,直线PF1:
,直线PF1: ,则
,则 ,由此能求出
,由此能求出 的值.
的值.解答:解:(1)△F1F2P中,|F1F2|=2c∠F1PF2=60°
∴
 …(2分)
…(2分)∴
 ,
,∴
 …(5分)
…(5分)(2)∵
 ,
,∴b2=2a2,
设双曲线方程为
 ,
,即2x2-y2=2a2,①…(7分)
直线PF1:
 ,
,即
 ,②…(8分)
,②…(8分)由①②得

∴
 …(11分)
…(11分)再由双曲线的渐进线方程2x2-y2=0,
∴|AB|=
 ,
,∴
 .…(13分)
.…(13分)点评:题主要考查双曲线标准方程,简单几何性质,直线与双曲线的位置关系等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (文)如图,已知矩形ACEF的边CE与正方形ABCD所在平面垂直,
(文)如图,已知矩形ACEF的边CE与正方形ABCD所在平面垂直,