题目内容
曲线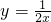 和y=ax2在它们的交点处的两条切线互相垂直,则实数a的值是
和y=ax2在它们的交点处的两条切线互相垂直,则实数a的值是
- A.

- B.

- C.

- D.不存在
C
分析:先求出它们交点的横坐标,再求出它们的斜率表达式,由两条切线互相垂直、斜率之积等于-1,解出a的值.
解答:曲线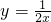 和y=ax2的交点的横坐标是
和y=ax2的交点的横坐标是 ,
,
两条切线的斜率分别是 =-
=- 和 2ax=2a•
和 2ax=2a• ,
,
∵切线互相垂直,
∴- •2a•
•2a• =-1,
=-1,
∴a= ,
,
故选C.
点评:本题考查利用导数研究曲线上某点切线方程、两条直线垂直的条件,属于基础题.
分析:先求出它们交点的横坐标,再求出它们的斜率表达式,由两条切线互相垂直、斜率之积等于-1,解出a的值.
解答:曲线
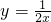 和y=ax2的交点的横坐标是
和y=ax2的交点的横坐标是 ,
,两条切线的斜率分别是
 =-
=- 和 2ax=2a•
和 2ax=2a• ,
,∵切线互相垂直,
∴-
 •2a•
•2a• =-1,
=-1,∴a=
 ,
,故选C.
点评:本题考查利用导数研究曲线上某点切线方程、两条直线垂直的条件,属于基础题.

练习册系列答案
相关题目
 和y=ax2在它们的交点处的两条切线互相垂直,则实数a的值是( )
和y=ax2在它们的交点处的两条切线互相垂直,则实数a的值是( )


 和y=x2在它们的交点处的两条切线与x轴所围成的三角形的面积是 .
和y=x2在它们的交点处的两条切线与x轴所围成的三角形的面积是 .