题目内容
14.设△ABC的内角A,B,C的对边分别为a,b,c,a=btanA.(Ⅰ)证明:sinB=cosA;
(Ⅱ)若sinC-sinAcosB=$\frac{3}{4}$,且B为钝角,求A,B,C.
分析 (Ⅰ)由正弦定理及已知可得$\frac{sinA}{sinB}$=$\frac{sinA}{cosA}$,由sinA≠0,即可证明sinB=cosA.
(Ⅱ)由两角和的正弦函数公式化简已知可得sinC-sinAcosB=cosAsinB=$\frac{3}{4}$,由(1)sinB=cosA,可得sin2B=$\frac{3}{4}$,结合范围可求B,由sinB=cosA及A的范围可求A,由三角形内角和定理可求C.
解答 解:(Ⅰ)证明:∵a=btanA.
∴$\frac{a}{b}$=tanA,
∵由正弦定理:$\frac{a}{b}=\frac{sinA}{sinB}$,又tanA=$\frac{sinA}{cosA}$,
∴$\frac{sinA}{sinB}$=$\frac{sinA}{cosA}$,
∵sinA≠0,
∴sinB=cosA.得证.
(Ⅱ)∵sinC=sin[π-(A+B)]=sin(A+B)=sinAcosB+cosAsinB,
∴sinC-sinAcosB=cosAsinB=$\frac{3}{4}$,由(1)sinB=cosA,
∴sin2B=$\frac{3}{4}$,
∵0<B<π,
∴sinB=$\frac{\sqrt{3}}{2}$,
∵B为钝角,
∴B=$\frac{2π}{3}$,
又∵cosA=sinB=$\frac{\sqrt{3}}{2}$,
∴A=$\frac{π}{6}$,
∴C=π-A-B=$\frac{π}{6}$,
综上,A=C=$\frac{π}{6}$,B=$\frac{2π}{3}$.
点评 本题主要考查了正弦定理,三角形内角和定理,两角和的正弦函数公式的应用,属于基础题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
4.已知定义在(-3,3)上的函数f(x)满足f(x-1)=-f(1-x),且x≥0时,f(x)=x3,则f(x)+27f(1-x)>0的解集为( )
| A. | ∅ | B. | (-3,$\frac{1}{2}$) | C. | (-2,$\frac{3}{2}$) | D. | ($\frac{3}{2}$,3) |
2.某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( )
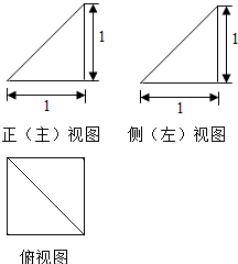

| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
9.若实数a,b满足$\frac{1}{a}$+$\frac{2}{b}$=$\sqrt{ab}$,则ab的最小值为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
19. 一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )
一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )
 一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )
一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{7}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{5}$ |
6. 某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
A地区:62 73 81 92 95 85 74 64 53 76
78 86 95 66 97 78 88 82 76 89
B地区:73 83 62 51 91 46 53 73 64 82
93 48 65 81 74 56 54 76 65 79
(1)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);
(2)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
记事件C:“A地区用户的满意度等级高于B地区用户的满意度等级”,假设两地区用户的评价结果相互独立,根据所给数据,以事件发生的频率作为相应事件发生的频率,求C的概率.
 某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:A地区:62 73 81 92 95 85 74 64 53 76
78 86 95 66 97 78 88 82 76 89
B地区:73 83 62 51 91 46 53 73 64 82
93 48 65 81 74 56 54 76 65 79
(1)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);
(2)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
| 满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
| 满意度等级 | 不满意 | 满意 | 非常满意 |
3.已知点A(0,1),B(3,2),向量$\overrightarrow{AC}$=(-4,-3),则向量$\overrightarrow{BC}$=( )
| A. | (-7,-4) | B. | (7,4) | C. | (-1,4) | D. | (1,4) |