题目内容
(本题15分)已知曲线C是到点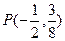 和到直线
和到直线
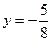 距离相等的点的轨迹,l是过点Q(-1,0)的直线,
距离相等的点的轨迹,l是过点Q(-1,0)的直线,
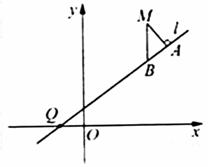
M是C上(不在l上)的动点;A、B在l上,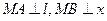
轴(如图)。
(Ⅰ)求曲线C的方程;
(Ⅱ)求出直线l的方程,使得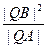 为常数。
为常数。
 和到直线
和到直线
 距离相等的点的轨迹,l是过点Q(-1,0)的直线,
距离相等的点的轨迹,l是过点Q(-1,0)的直线,M是C上(不在l上)的动点;A、B在l上,
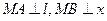
轴(如图)。
(Ⅰ)求曲线C的方程;
(Ⅱ)求出直线l的方程,使得
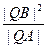 为常数。
为常数。(Ⅰ) ,(Ⅱ)
,(Ⅱ)
 ,(Ⅱ)
,(Ⅱ)
本题主要考查求曲线轨迹方程,两条直线的位置关系等基础知识,考查解析几何的基本思想方法和综合解题能力。满分15分。


(I)设 为C上的点,则
为C上的点,则
 .
.
N到直线 的距离为
的距离为 .
.
由题设得 .
.
化简,得曲线C的方程为 .
.
(II)解法一:
设 ,直线l:
,直线l: ,则
,则 ,从而
,从而
 .
.
在Rt△QMA中,因为
 ,
,
 .
.
所以
 ,
,

当k=2时,
从而所求直线l方程为
解法二:
设 ,直线直线l:
,直线直线l: ,则
,则 ,从而
,从而

过 垂直于l的直线l1:
垂直于l的直线l1: ,
,
因为 ,所以
,所以
 ,
,
 ,
,
当k=2时, ,
,
从而所求直线l方程为


(I)设
 为C上的点,则
为C上的点,则 .
.N到直线
 的距离为
的距离为 .
.由题设得
 .
.化简,得曲线C的方程为
 .
.(II)解法一:
设
 ,直线l:
,直线l: ,则
,则 ,从而
,从而 .
.在Rt△QMA中,因为
 ,
,  .
.所以

 ,
,
当k=2时,

从而所求直线l方程为

解法二:
设
 ,直线直线l:
,直线直线l: ,则
,则 ,从而
,从而
过
 垂直于l的直线l1:
垂直于l的直线l1: ,
,因为
 ,所以
,所以 ,
, ,
,当k=2时,
 ,
,从而所求直线l方程为


练习册系列答案
相关题目
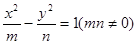 离心率为2,有一个焦点与抛物线
离心率为2,有一个焦点与抛物线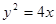 的焦点重
的焦点重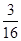
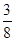
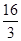
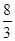
 ,y
,y )、B(x
)、B(x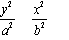 (a > b > 0) 上的两点,
(a > b > 0) 上的两点,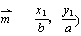 ,
,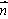 = (
= (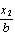 ,
,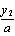 ),且满足
),且满足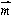 ·
·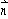 = 0,椭圆的离心率e =
= 0,椭圆的离心率e = 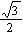 ,短轴长为2,O为坐标原点.(1)求椭圆的方程;(2)若存在斜率为k的直线AB过椭圆的焦点F(0,c)(c为半焦距),求直线AB的斜率k的值.
,短轴长为2,O为坐标原点.(1)求椭圆的方程;(2)若存在斜率为k的直线AB过椭圆的焦点F(0,c)(c为半焦距),求直线AB的斜率k的值.


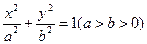 上
上 的一个动点,弦AB、AC分别过焦点
的一个动点,弦AB、AC分别过焦点
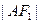 ∶
∶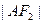 =3∶1.(1)求该椭圆的离心率;
=3∶1.(1)求该椭圆的离心率;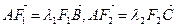 ,试判断
,试判断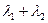 是否为定值?若是,则求出该定值;若不是,请说明理由。
是否为定值?若是,则求出该定值;若不是,请说明理由。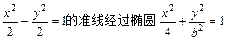 (b>0)的焦点,则b=()
(b>0)的焦点,则b=()
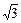
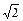


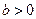 ,椭圆方程为
,椭圆方程为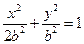 ,抛物线方程为
,抛物线方程为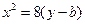 .如图6所示,过点
.如图6所示,过点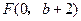 作
作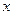 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为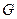 ,已知抛物线在点
,已知抛物线在点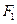 .
.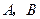 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点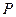 ,使得
,使得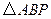 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).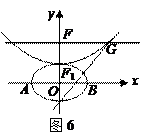
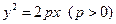 的焦点与双曲线
的焦点与双曲线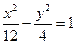 的右焦点重合,则
的右焦点重合,则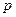 的值为C
的值为C .
. 
 .
. 
 .
. 
 .
.