题目内容
设函数g(x)=g( )lnx+1,则g(e)=________.(其中e为自然对数的底数)
)lnx+1,则g(e)=________.(其中e为自然对数的底数)
1
分析:由g(x)=g( )lnx+1,知
)lnx+1,知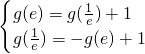 ,由此能求出g(e).
,由此能求出g(e).
解答:∵g(x)=g( )lnx+1,
)lnx+1,
∴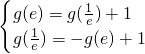 ,
,
解得g(e)=1.
故答案为:1.
点评:本题考查函数值的求法,是基础题.解题时要认真审题,仔细解答.
分析:由g(x)=g(
 )lnx+1,知
)lnx+1,知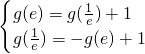 ,由此能求出g(e).
,由此能求出g(e).解答:∵g(x)=g(
 )lnx+1,
)lnx+1,∴
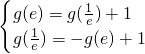 ,
,解得g(e)=1.
故答案为:1.
点评:本题考查函数值的求法,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目