题目内容
如图，在平面四边形ABCD中，AB=AD=1，∠BAD=θ；而△BCD是正三角形．(Ⅰ)将四边形ABCD面积S表示为θ的函数；
(Ⅱ)求S的最大值及此时θ角的值．
解：(Ⅰ)△ABD的面积
S=
|AB|·IADI·sinA=
·1·1sinθ=
sinθ
∵△BDC是正三角形，则△BDC面积为
BD2
而由△ABD及余弦定理可知：
BD2=12+12-2·1·1·cosθ=2-2cosθ
于是四边形ABCD面积S=
sinθ+
(2-2cosθ)
S=
+sin(θ-
)其中0＜θ＜π
(Ⅱ)由S=
+sin(θ-
)及0＜θ＜π
则-
＜θ-
＜
在θ-
=
时， S取得最大值1+
此时θ=
+
=
练习册系列答案
相关题目
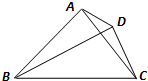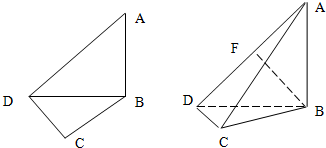
如图，在平面四边形ABCD中，若AB=2，CD=1，则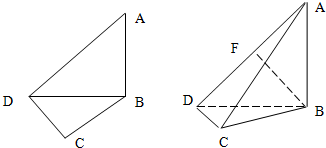
如图，在平面四边形ABCD中，已知∠A=45°，∠C=90°，∠ADC=105°，AB=BD，现将四边形ABCD沿BD折起，使平面ABD⊥平面BDC，设点F为棱AD的中点．
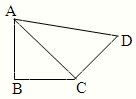如图，在平面四边形ABCD中，AB=BC=CD=a，∠ABC=90°，∠BCD=135°，沿对角线AC将此四边形折成直二面角．
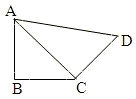如图，在平面四边形ABCD中，AB=BC=CD=a，∠ABC=90°，∠BCD=135°，沿对角线AC将此四边形折成直二面角．