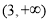题目内容
17.已知函数f(x)=log3(a-2x)的定义域为D,若(-∞,-3)⊆D,则实数a的取值范围是( )| A. | (-∞,-6) | B. | (-∞,-6] | C. | (-6,+∞) | D. | [-6,+∞) |
分析 先求出f(x)的定义域D(-∞,$\frac{a}{2}$),再利用(-∞,-3)⊆D得出-3与$\frac{a}{2}$的关系,从而求出答案.
解答 解:由f(x)=log3(a-2x)有意义得:
a-2x>0.
解得:x<$\frac{a}{2}$,即f(x)的定义域为D=(-∞,$\frac{a}{2}$).
∵(-∞,-3)⊆D
∴-3≤$\frac{a}{2}$,即a≥-6.
故选D.
点评 本题考查了对数函数的定义域,集合间的关系,属于基础题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
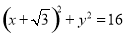 ,动圆N过点F
,动圆N过点F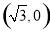 且与圆M相切,记圆心N的轨迹为E.
且与圆M相切,记圆心N的轨迹为E. ,在约束条件
,在约束条件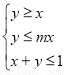 下,目标函数
下,目标函数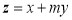 的最大值小于2,则
的最大值小于2,则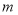 的取值范围为
的取值范围为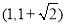 B.
B.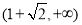 C.
C.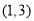 D.
D.