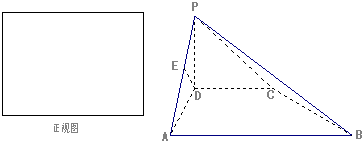
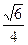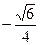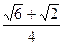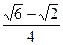题目内容
如图所示,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
(1)证明:B1C1⊥CE;
(2)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为
.求线段AM的长.
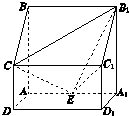
(1)证明:B1C1⊥CE;
(2)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为
| ||
| 6 |

(1)证明:因为侧棱CC1⊥平面A1B1C1D1,B1C1?平面A1B1C1D1,
所以CC1⊥B1C1.
因为AD=CD=1,AA1=AB=2,E为棱AA1的中点,
所以B1E=
,B1C1=
,EC1=
,
从而B1E2=B1C
+EC
,
所以在△B1EC1中,B1C1⊥C1E.
又CC1,C1E?平面CC1E,CC1∩C1E=C1,
所以B1C1⊥平面CC1E,
又CE?平面CC1E,故B1C1⊥CE.
(2)连结D1E,过点M作MH⊥ED1于点H,可得MH⊥平面ADD1A1,
连结AH,AM,则∠MAH为直线AM与平面ADD1A1所成的角.
设AM=x,从而在Rt△AHM中,有MH=
x,AH=
x.
在Rt△C1D1E中,C1D1=1,ED1=
,得EH=
MH=
x.
在△AEH中,∠AEH=135°,AE=1,由AH2=AE2+EH2-2AE•EHcos135°,得
x2=1+
x2+
x.
整理得5x2-2
x-6=0,解得x=
(负值舍去),
所以线段AM的长为
.

所以CC1⊥B1C1.
因为AD=CD=1,AA1=AB=2,E为棱AA1的中点,
所以B1E=
| 5 |
| 2 |
| 3 |
从而B1E2=B1C
| 21 |
| 21 |
所以在△B1EC1中,B1C1⊥C1E.
又CC1,C1E?平面CC1E,CC1∩C1E=C1,
所以B1C1⊥平面CC1E,
又CE?平面CC1E,故B1C1⊥CE.
(2)连结D1E,过点M作MH⊥ED1于点H,可得MH⊥平面ADD1A1,
连结AH,AM,则∠MAH为直线AM与平面ADD1A1所成的角.
设AM=x,从而在Rt△AHM中,有MH=
| ||
| 6 |
| ||
| 6 |
在Rt△C1D1E中,C1D1=1,ED1=
| 2 |
| 2 |
| 1 |
| 3 |
在△AEH中,∠AEH=135°,AE=1,由AH2=AE2+EH2-2AE•EHcos135°,得
| 17 |
| 18 |
| 1 |
| 9 |
| ||
| 3 |
整理得5x2-2
| 2 |
| 2 |
所以线段AM的长为
| 2 |


练习册系列答案
相关题目
 为其圆心)上,且点A、C、D、
为其圆心)上,且点A、C、D、 ,则异面直线AB与CD所成角的余弦值为 ( )
,则异面直线AB与CD所成角的余弦值为 ( )