题目内容
(2007•武汉模拟)正四棱锥S-ABCD内接于一个半径为R的球,那么这个正四棱锥体积的最大值为
R3
R3.
| 64 |
| 81 |
| 64 |
| 81 |
分析:先设正四棱锥S-ABCD的底面边长等于a,底面到球心的距离等于x,得到x与a,R之间的关系,又正四棱锥的高为h=R+x
从而得出正四棱锥体积关于x函数表达式,最后利用基本不等式求出这个正四棱锥体积的最大值即可.
从而得出正四棱锥体积关于x函数表达式,最后利用基本不等式求出这个正四棱锥体积的最大值即可.
解答:解:设正四棱锥S-ABCD的底面边长等于a,底面到球心的距离等于x
则:x2+(
a) 2=R 2
而正四棱锥的高为h=R+x
故正四棱锥体积为:
V(x)=
×a2h=
×a2(R+x)=
(R 2-x 2)(R+x)
其中x∈(0,R)
∵
(R 2-x 2)(R+x) =
(2R-2x)(R+x)(R+x)≤
×(
) 3=
R3
当且仅当x=
R时,等号成立
那么这个正四棱锥体积的最大值为:
R3
故答案为:
R3
则:x2+(
| ||
| 2 |
而正四棱锥的高为h=R+x
故正四棱锥体积为:
V(x)=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
其中x∈(0,R)
∵
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| (2R-2x)+(R+x)+(R+x) |
| 3 |
| 64 |
| 81 |
当且仅当x=
| 1 |
| 3 |
那么这个正四棱锥体积的最大值为:
| 64 |
| 81 |
故答案为:
| 64 |
| 81 |
点评:本题主要考查了球内接多面体、棱柱、棱锥、棱台的体积等基本知识,考查了空间想象力,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
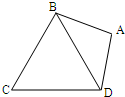 (2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形,
(2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形, (2007•武汉模拟)如图,直线l:y=
(2007•武汉模拟)如图,直线l:y=