题目内容
（2012•道里区三模）选修4-4：坐标系与参数方程
在直角坐标系xOy中，过点P(
，
)作倾斜角为α的直线l与曲线C：x2+y2=1相交于不同的两点M，N．
（Ⅰ） 写出直线l的参数方程；
（Ⅱ） 求
+
的取值范围．
在直角坐标系xOy中，过点P(
| ||
| 2 |
| 3 |
| 2 |
（Ⅰ） 写出直线l的参数方程；
（Ⅱ） 求
| 1 |
| |PM| |
| 1 |
| |PN| |
分析：（Ⅰ）利用直线的参数方程的意义即可写出；
（Ⅱ）把直线的参数方程代入圆的方程，利用根与系数的关系即可求出．
（Ⅱ）把直线的参数方程代入圆的方程，利用根与系数的关系即可求出．
解答：解：（Ⅰ）∵直线l过点P(
，
)且倾斜角为α，
∴直线l的参数方程为
（t为参数）；
（Ⅱ）把
（t为参数）代入x2+y2=1，
得t2+(
cosα+3sinα)t+2=0，
∵直线l与曲线C：x2+y2=1相交于不同的两点M，N，
∴△=(
cosα+3sinα)2-8＞0，
化为sin(α+
)＞
．
又t1+t2=-(
cosα+3sinα)，t1t2=2．
∴
+
=-(
+
)=-
=
=
sin(α+
)，
∵sin(α+
)＞
，∴
＜
sin(α+
)≤
．
∴
+
的取值范围是(
，
]．
| ||
| 2 |
| 3 |
| 2 |
∴直线l的参数方程为
|
（Ⅱ）把
|
得t2+(
| 3 |
∵直线l与曲线C：x2+y2=1相交于不同的两点M，N，
∴△=(
| 3 |
化为sin(α+
| π |
| 6 |
| ||
| 3 |
又t1+t2=-(
| 3 |
∴
| 1 |
| |PM| |
| 1 |
| |PN| |
| 1 |
| t1 |
| 1 |
| t2 |
| t1+t2 |
| t1t2 |
| ||
| 2 |
| 3 |
| π |
| 6 |
∵sin(α+
| π |
| 6 |
| ||
| 3 |
| 2 |
| 3 |
| π |
| 6 |
| 3 |
∴
| 1 |
| |PM| |
| 1 |
| |PN| |
| 2 |
| 3 |
点评：熟练直线的参数方程及其几何意义、一元二次方程的根与系数的关系是解决问题的关键．
练习册系列答案
特高级教师点拨系列答案
相关题目
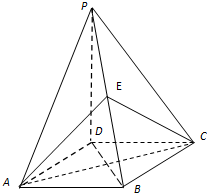（2012•道里区三模）如图，四棱锥P-ABCD的底面是正方形，PD⊥底面ABCD，点E在棱PB上．
（2012•道里区三模）如图，设D是图中边长分别为1和2的矩形区域，E是D内位于函数y=