题目内容
某联欢晚会举行抽奖活动,举办方设置了甲.乙两种抽奖方案,方案甲的中奖率为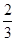 ,中将可以获得2分;方案乙的中奖率为
,中将可以获得2分;方案乙的中奖率为 ,中将可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中将与否互不影响,晚会结束后凭分数兑换奖品.
,中将可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中将与否互不影响,晚会结束后凭分数兑换奖品.
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为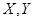 ,求
,求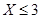 的概率;
的概率;
(2)若小明.小红两人都选择方案甲或方案乙进行抽奖,问:他们选择何种方案抽奖,累计的得分的数学期望较大?
(1)
(2)选择方案甲进行抽奖时,累计得分的数学期望最大
解析试题分析:解:(Ⅰ)由已知得:小明中奖的概率为 ,小红中奖的概率为
,小红中奖的概率为 ,两人中奖与否互不影响,
,两人中奖与否互不影响,
记“这2人的累计得分 ”的事件为A,则A事件的对立事件为“
”的事件为A,则A事件的对立事件为“ ”,
”,  ,
,
 这两人的累计得分
这两人的累计得分 的概率为
的概率为 . 6分
. 6分
(Ⅱ)设小明.小红都选择方案甲抽奖中奖的次数为 ,都选择方案乙抽奖中奖的次数为
,都选择方案乙抽奖中奖的次数为 ,则这两人选择方案甲抽奖累计得分的数学期望为
,则这两人选择方案甲抽奖累计得分的数学期望为 ,选择方案乙抽奖累计得分的数学期望为
,选择方案乙抽奖累计得分的数学期望为
由已知: ,
,
 ,
,
 ,
,

 他们都在选择方案甲进行抽奖时,累计得分的数学期望最大. 12分
他们都在选择方案甲进行抽奖时,累计得分的数学期望最大. 12分
考点:独立事件的概率以及期望
点评:主要是考查了独立事件的概率以及期望值的运用,属于中档题。

 口算能手系列答案
口算能手系列答案为了对某课题进行研究,用分层抽样方法从三所科研单位A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人):
| 科研单位 | 相关人数 | 抽取人数 |
| A | 16 | 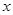 |
| B | 12 | 3 |
| C | 8 | 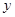 |
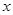 与
与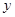 的值;
的值;(2)若从科研单位A、C抽取的人中选2人作专题发言,求这2人都来自科研单位A的概率.
随着经济的发展,人们生活水平的提高,中学生的营养与健康问题越来越得到学校与家长的重视. 从学生体检评价报告单了解到某校3000名学生的体重发育评价情况,得右表:
| | 偏瘦 | 正常 | 肥胖 |
| 女生(人) | 300 | 865 |  |
| 男生(人) | 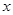 | 885 | 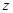 |
(Ⅰ)求
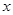 的值;
的值;(Ⅱ)若用分层抽样的方法,从这批学生中随机抽取60名,问应在肥胖学生中抽出多少名?
(Ⅲ)已知
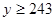 ,
,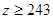 ,求肥胖学生中男生不少于女生的概率.
,求肥胖学生中男生不少于女生的概率. 根据以往资料统计,大学生购买某品牌平板电脑时计划采用分期付款的期数ζ的分布列为
| ζ | 1 | 2 | 3 |
| P | 0.4 | 0.25 | 0.35 |
(2)若签订协议后,在实际付款中,采用1期付款的没有变化,采用2、3期付款的都至多有一次改付款期数的机会,其中采用2期付款的只能改为3期,概率为
 ;采用3期付款的只能改为2期,概率为
;采用3期付款的只能改为2期,概率为 .数码城销售一台该平板电脑,实际付款期数
.数码城销售一台该平板电脑,实际付款期数 与利润
与利润 (元)的关系为
(元)的关系为 | 1 | 2 | 3 |
| η | 200 | 250 | 300 |
 的分布列及期望E(
的分布列及期望E( ).
). 为了对某课题进行研究,用分层抽样的方法从 三所高校的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人).
三所高校的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人).
| 高校 | 相关人数 | 抽取人数 |
 | 18 |  |
 | 36 |  |
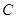 | 54 |  |
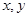 ;
;(2) 若从高校
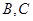 抽取的人中选2人作专题发言,求这2人都来自高校
抽取的人中选2人作专题发言,求这2人都来自高校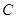 的概率.
的概率.  箱中有3个黑球,6个白球,每个球被取到的概率相同,
箱中有3个黑球,6个白球,每个球被取到的概率相同,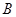 箱中没有球.我们把从
箱中没有球.我们把从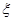 ,求
,求 次,每次相互独立;
次,每次相互独立;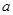 ,再由乙猜测甲写的数字,记为
,再由乙猜测甲写的数字,记为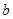 ,已知
,已知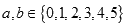 ,若
,若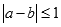 ,则本次竞猜成功;
,则本次竞猜成功;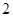 次竞猜成功,则两人获奖.
次竞猜成功,则两人获奖. 人组成的代表队中选
人组成的代表队中选 人参加此游戏,这
人参加此游戏,这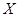 ,求
,求