题目内容
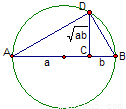
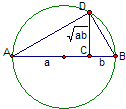设AB是已知圆的直径（如图），C是线段AB上一点，D是此圆周上一点（不同于A、B），且|AC|=a，|BC|=b，|CD|=| ab |
分析：对于A，利用基本不等式可知正确；对于B，利用相交弦定理，可判断正确；对于C，AB是已知圆的直径，所以AD⊥BD；对于D，利用勾股定理，结合基本不等式可判断．
解答：解：∵|AB|=a+b≥2
=2|CD|，∴A正确；
延长DC至E，则AC×CB=DC×CE，∵|AC|=a，|BC|=b，|CD|=
，∴CE=
，
∴C是DE的中点，∴AB⊥CD，∴
•
=0，故B正确；
∵AB是已知圆的直径，∴AD⊥BD，∴
•
=0，故C正确；
∵AD|2+|BD|2=|AB|2=（a+b）2=a2+b2+2ab≥2ab+2ab=4ab=4|CD|2，故D不正确；
故选D．
| ab |
延长DC至E，则AC×CB=DC×CE，∵|AC|=a，|BC|=b，|CD|=
| ab |
| ab |
∴C是DE的中点，∴AB⊥CD，∴
| AB |
| CD |
∵AB是已知圆的直径，∴AD⊥BD，∴
| AD |
| BD |
∵AD|2+|BD|2=|AB|2=（a+b）2=a2+b2+2ab≥2ab+2ab=4ab=4|CD|2，故D不正确；
故选D．
点评：本题以圆为载体，考查直角三角形的射影定理，解题的关键是结合圆中的性质，利用基本不等式求解
练习册系列答案
相关题目
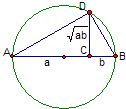设AB是已知圆的直径（如图），C是线段AB上一点，D是此圆周上一点（不同于A、B），且
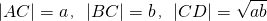，则在下列结论中错误的是
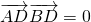
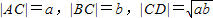，则在下列结论中错误的是（ ）
