题目内容
已知f(x)=|log3x|,当0<a<2时,有f(a)>f(2),则a的求值范围是分析:由已知中函数f(x)=|log3x|,我们可以判断出函数的单调性,进而根据对数的性质,解不等式f(a)>f(2),得到a的取值范围,结合0<a<2,即可得到答案.
解答:解:∵f(x)=|log3x|,
∴函数在(0,1)上单调递减,在(1,+∞)上单调递增
若f(a)>f(2),则0<a<
,或a>2,
又由0<a<2
∴满足条件的a的取值范围为0<a<
故答案为:0<a<
∴函数在(0,1)上单调递减,在(1,+∞)上单调递增
若f(a)>f(2),则0<a<
| 1 |
| 2 |
又由0<a<2
∴满足条件的a的取值范围为0<a<
| 1 |
| 2 |
故答案为:0<a<
| 1 |
| 2 |
点评:本题考查的知识点是对数函数的单调性与特殊点,绝对值函数的性质,对数不等式的解法,其中根据绝对值函数图象的对折变换法则和对数函数的性质,判断出函数的单调性是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
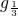 [3-(x-1)2],求f(x)的值域及单调区间.
[3-(x-1)2],求f(x)的值域及单调区间. [3-(x-1)2],求f(x)的值域及单调区间.
[3-(x-1)2],求f(x)的值域及单调区间.