题目内容
7.已知a,b>0,且a+b=1,求:(Ⅰ)$\frac{1}{a^2}$+$\frac{1}{b^2}$的最小值;
(Ⅱ)$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{ab}$的最小值.
分析 (Ⅰ)出现条件中和为定值,求函数中含有积的最值用基本不等式进行解答,即:ab≤($\frac{a+b}{2}$)2,则$\frac{1}{a^2}$+$\frac{1}{b^2}$≥$\frac{2}{ab}$,由此求得最值;
(Ⅱ)将$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{ab}$变形为2(a+b)($\frac{1}{a}$+$\frac{1}{b}$)=4+2($\frac{b}{a}$+$\frac{a}{b}$),所以利用基本不等式进行解答.
解答 解:(Ⅰ)∵ab≤($\frac{a+b}{2}$)2=$\frac{1}{4}$,
∴当且仅当a=b时等号成立,
∵a+b=1,a=b=$\frac{1}{2}$,
∴$\frac{1}{ab}$≥4.
∵$\frac{1}{a^2}$+$\frac{1}{b^2}$≥$\frac{2}{ab}$≥8,当且仅当a=b=$\frac{1}{2}$时等号成立,
∴$\frac{1}{a^2}$+$\frac{1}{b^2}$≥8.
(Ⅱ)∵$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{ab}$
=$\frac{1}{a}$+$\frac{1}{b}$+$\frac{a+b}{ab}$
=$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{a}$+$\frac{1}{b}$
=2(a+b)($\frac{1}{a}$+$\frac{1}{b}$)
=4+2($\frac{b}{a}$+$\frac{a}{b}$)
≥4+4$\sqrt{\frac{b}{a}•\frac{a}{b}}$=8,当且仅当a=b=$\frac{1}{2}$时等号成立,
∴$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{ab}$≥8.
点评 本题考查了基本不等式. 基本不等式主要应用于求某些函数的最值及证明不等式.其可表述为:两个正实数的几何平均数小于或等于它们的算术平均数.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案| A. | f(x)没有零点 | B. | f(x)有极小值点 | C. | f(x)有极大值点 | D. | f(x)没有极值点 |
 如图,有一条长为50$\sqrt{2}$(米)的斜坡AB,它的坡角为45°,现保持坡高AC不变,将坡角改为30°,则斜坡AD的长为100(米).
如图,有一条长为50$\sqrt{2}$(米)的斜坡AB,它的坡角为45°,现保持坡高AC不变,将坡角改为30°,则斜坡AD的长为100(米).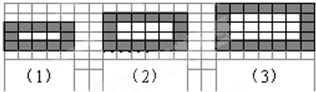 如图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第1846个图案中需用黑色瓷砖7392块.
如图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第1846个图案中需用黑色瓷砖7392块.