题目内容
(2012•梅州二模)己知点A(1,0),B(0,1),C(2sinθ,cosθ).
(1)若(
+2
)•
=1,其中O为坐标原点,求sin2θ的值;
(2)若|
|=|
|,且θ在第三象限.求sin(θ+
)值.
(1)若(
| OA |
| OB |
| OC |
(2)若|
| AC |
| BC |
| π |
| 3 |
分析:(1)由 (
+2
)•
=1解得sinθ+cosθ=
,平方求得sin2θ 的值.
(2)由 |
|=|
|,且θ在第三象限可得sinθ=-
,cosθ=-
,再利用两角和的正弦公式求得 sin(θ+
)的值.
| OA |
| OB |
| OC |
| 1 |
| 2 |
(2)由 |
| AC |
| BC |
| ||
| 5 |
2
| ||
| 5 |
| π |
| 3 |
解答:解:(1)∵(
+2
)•
=(1,2)•(2sinθ,cosθ)=2sinθ+2cosθ=1,
∴sinθ+cosθ=
,∴(sinθ+cosθ)2=1+sin2θ=
,故sin2θ=-
.
(2)∵
=(2sinθ-1,cosθ),
=(2sinθ,cosθ-1),|
|=|
|,且θ在第三象限
∴(2sinθ-1)2+cos2θ=(2sinθ)2+(cosθ-1)2,
解得 sinθ=-
,cosθ=-
.
∴sin(θ+
)=sinθcos
+cosθsin
=
.
| OA |
| OB |
| OC |
∴sinθ+cosθ=
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
(2)∵
| AC |
| BC |
| AC |
| BC |
∴(2sinθ-1)2+cos2θ=(2sinθ)2+(cosθ-1)2,
解得 sinθ=-
| ||
| 5 |
2
| ||
| 5 |
∴sin(θ+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| ||||
| 10 |
点评:本题主要考查三角函数的恒等变换及化简求值,两个向量的数量积的坐标运算,两个向量数量积公式,属于中档题.

练习册系列答案
相关题目
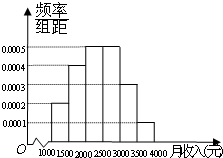 (2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).
(2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).