题目内容
(2012•梅州二模)设a,b∈R,若复数z=
,则z在复平面上对应的点在( )
| 1+2i |
| 1+i |
分析:利用复数的代数形式的乘除运算,得到z=
=-
+
i.由此能求出z在复平面上对应的点(-
,
)所在象限.
| 1+2i |
| 1+i |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵z=
=
=
=
=-
+
i.
∴z在复平面上对应的点(-
,
)在第二象限.
故选B.
| 1+2i |
| 1+i |
=
| (1+2i)(1-i) |
| (1+i)(1-i) |
=
| 1+2i-i-2i2 |
| 2 |
=
| -1+i |
| 2 |
=-
| 1 |
| 2 |
| 1 |
| 2 |
∴z在复平面上对应的点(-
| 1 |
| 2 |
| 1 |
| 2 |
故选B.
点评:本题考查复数的代数形式的乘除运算,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
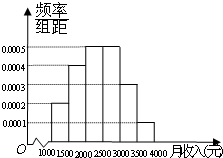 (2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).
(2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).