题目内容
【题目】某制造厂商10月份生产了一批乒乓球,从中随机抽取![]() 个进行检查,测得每个球的直径(单位:
个进行检查,测得每个球的直径(单位:![]() ),将数据进行分组,得到如下频率分布表:
),将数据进行分组,得到如下频率分布表:
(1)求![]() 、
、![]() 、
、![]() 及
及![]() 、
、![]() 的值,并画出频率分布直方图(结果保留两位小数);
的值,并画出频率分布直方图(结果保留两位小数);
(2)已知标准乒乓球的直径为![]() ,且称直径在
,且称直径在![]() 内的乒乓球为五星乒乓球,若这批乒乓球共有
内的乒乓球为五星乒乓球,若这批乒乓球共有![]() 个,试估计其中五星乒乓球的数目;
个,试估计其中五星乒乓球的数目;
(3)统计方法中,同一组数据常用该组区间的中点值(例如区间![]() 的中点值是
的中点值是![]() )作为代表,试估计这批乒乓球直径的平均值和中位数.
)作为代表,试估计这批乒乓球直径的平均值和中位数.
【答案】(1)见解析,(2)5000,(3)平均数为39.996,中位数为![]() .
.
【解析】
试题分析: (1)根据频率等于频数除以总数,先求总数![]() ,再求
,再求![]() 对应频数
对应频数![]() ,根据频数和为总数得
,根据频数和为总数得![]() ,最后再根据频率等于频数除以总数,得
,最后再根据频率等于频数除以总数,得![]() 、
、![]() 的值,以频率除以组距作为对应区间纵坐标画出频率分布直方图,(2)直径在
的值,以频率除以组距作为对应区间纵坐标画出频率分布直方图,(2)直径在![]() 内对应概率为
内对应概率为![]() ,根据频数等于总数乘以频率,得频数,(3)由平均值为各组中点值与对应概率乘积的和,得平均值;中位数必在区间
,根据频数等于总数乘以频率,得频数,(3)由平均值为各组中点值与对应概率乘积的和,得平均值;中位数必在区间![]() 内,由频率关系列等量关系:设中位数为
内,由频率关系列等量关系:设中位数为![]() ,则有
,则有![]() ,解方程可得中位数.
,解方程可得中位数.
试题解析:(1)由频率分布表可知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
频率分布直方图如图:
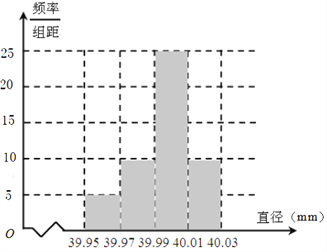
(2)因为五星乒乓球的直径在![]() 内,所以由频率分布表,可得五星乒乓球的频率为
内,所以由频率分布表,可得五星乒乓球的频率为![]() ,(6分)
,(6分)
故![]() 个乒乓球中,“五星乒乓球”大约有
个乒乓球中,“五星乒乓球”大约有![]() (个).
(个).
(3)平均数![]() .
.
设中位数为![]() ,则
,则![]() 且
且![]() ,解得
,解得![]() .故中位数为
.故中位数为![]() .
.

练习册系列答案
相关题目

