题目内容
已知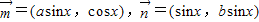 ,其中a,b,x∈R.若f(x)=
,其中a,b,x∈R.若f(x)=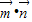 满足f(
满足f(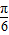 )=2,且f(x)的图象关于直线x=
)=2,且f(x)的图象关于直线x= 对称.
对称.(Ⅰ)求a,b的值;
(Ⅱ)若关于x的方程f(x)+log2k=0在区间[0,
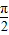 ]上总有实数解,求实数k的取值范围.
]上总有实数解,求实数k的取值范围.
【答案】分析:(I)由已知中 ,f(x)=
,f(x)= ,我们根据平面向量数量积公式,可以得到函数的解析式,(含参数a,b),进而根据f(
,我们根据平面向量数量积公式,可以得到函数的解析式,(含参数a,b),进而根据f( )=2,且f(x)的图象关于直线x=
)=2,且f(x)的图象关于直线x= 对称.我们可以构造关于a,b的方程,解方程即可求出a,b的值.
对称.我们可以构造关于a,b的方程,解方程即可求出a,b的值.
(II)若关于x的方程f(x)+log2k=0在区间[0, ]上总有实数解,我们可以求出函数f(x)在区间[0,
]上总有实数解,我们可以求出函数f(x)在区间[0, ]上的值域,构造一个对数不等式,解不等式即可求出实数k的取值范围.
]上的值域,构造一个对数不等式,解不等式即可求出实数k的取值范围.
解答:解:(Ⅰ) =
=
由 得,
得, ①
①
∵f(x)的图象关于 对称,∴
对称,∴ ∴
∴ ②
②
由①、②得,
(Ⅱ)由(Ⅰ)得 =
=
∵ ,
, ,
,
∴ ,f(x)∈[0,3].
,f(x)∈[0,3].
又∵f(x)+log2k=0有解,即f(x)=-log2k有解,
∴-3≤log2k≤0,解得 ,即
,即 .
.
点评:本题考查的知识点是函数y=Asin(ωx+φ)解析式的求法,正弦型函数的值域,及对数的性质,其中根据已知求出函数f(x)的解析式是解答本题的关键.
 ,f(x)=
,f(x)= ,我们根据平面向量数量积公式,可以得到函数的解析式,(含参数a,b),进而根据f(
,我们根据平面向量数量积公式,可以得到函数的解析式,(含参数a,b),进而根据f( )=2,且f(x)的图象关于直线x=
)=2,且f(x)的图象关于直线x= 对称.我们可以构造关于a,b的方程,解方程即可求出a,b的值.
对称.我们可以构造关于a,b的方程,解方程即可求出a,b的值.(II)若关于x的方程f(x)+log2k=0在区间[0,
 ]上总有实数解,我们可以求出函数f(x)在区间[0,
]上总有实数解,我们可以求出函数f(x)在区间[0, ]上的值域,构造一个对数不等式,解不等式即可求出实数k的取值范围.
]上的值域,构造一个对数不等式,解不等式即可求出实数k的取值范围.解答:解:(Ⅰ)
 =
=
由
 得,
得, ①
①∵f(x)的图象关于
 对称,∴
对称,∴ ∴
∴ ②
②由①、②得,

(Ⅱ)由(Ⅰ)得
 =
=
∵
 ,
, ,
,∴
 ,f(x)∈[0,3].
,f(x)∈[0,3].又∵f(x)+log2k=0有解,即f(x)=-log2k有解,
∴-3≤log2k≤0,解得
 ,即
,即 .
.点评:本题考查的知识点是函数y=Asin(ωx+φ)解析式的求法,正弦型函数的值域,及对数的性质,其中根据已知求出函数f(x)的解析式是解答本题的关键.

练习册系列答案
相关题目
已知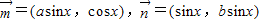 ,其中a,b,x∈R.若f(x)=
,其中a,b,x∈R.若f(x)=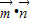 满足f(
满足f(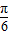 )=2,且f(x)的图象关于直线x=
)=2,且f(x)的图象关于直线x=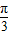 对称.
对称.
(Ⅰ)求a,b的值;
(Ⅱ)若关于x的方程f(x)+log2k=0在区间[0,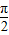 ]上总有实数解,求实数k的取值范围.
]上总有实数解,求实数k的取值范围.
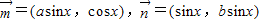 ,其中a,b,x∈R.若f(x)=
,其中a,b,x∈R.若f(x)=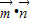 满足f(
满足f(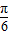 )=2,且f(x)的图象关于直线x=
)=2,且f(x)的图象关于直线x=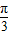 对称.
对称.(Ⅰ)求a,b的值;
(Ⅱ)若关于x的方程f(x)+log2k=0在区间[0,
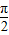 ]上总有实数解,求实数k的取值范围.
]上总有实数解,求实数k的取值范围.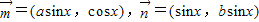 ,其中a,b,x∈R.若
,其中a,b,x∈R.若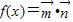 满足
满足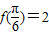 ,且f(x)的导函数f'(x)的图象关于直线
,且f(x)的导函数f'(x)的图象关于直线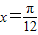 对称.
对称.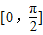 上总有实数解,求实数k的取值范围.
上总有实数解,求实数k的取值范围. ,其中a,b,x∈R.若f(x)=
,其中a,b,x∈R.若f(x)= 满足f(
满足f( )=2,且f(x)的图象关于直线x=
)=2,且f(x)的图象关于直线x= 对称.
对称. ]上总有实数解,求实数k的取值范围.
]上总有实数解,求实数k的取值范围.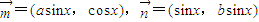 ,其中a,b,x∈R.若
,其中a,b,x∈R.若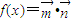 满足
满足 ,且f(x)的导函数f'(x)的图象关于直线
,且f(x)的导函数f'(x)的图象关于直线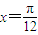 对称.
对称. 上总有实数解,求实数k的取值范围.
上总有实数解,求实数k的取值范围.