题目内容
【题目】已知椭圆的中心在原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点.
两点.
(1)若直线![]() 的斜率为1, 且
的斜率为1, 且![]() ,求椭圆的标准方程;
,求椭圆的标准方程;
(2)若(1)中椭圆的右顶点为![]() ,直线
,直线![]() 的倾斜角为
的倾斜角为![]() ,问
,问![]() 为何值时,
为何值时,![]() 取得最大值,并求出这个最大值.
取得最大值,并求出这个最大值.
【答案】(1) ![]() (2) 最大值为
(2) 最大值为![]() .
.
【解析】
试题(1)由题可设出椭圆方程;![]() ,先利用条件离心率为
,先利用条件离心率为![]() ,可推出
,可推出![]() 的关系。再结合过点
的关系。再结合过点![]() 且
且![]() 的直线与椭圆方程联立,并设出交点
的直线与椭圆方程联立,并设出交点![]() 的坐标,利用条件
的坐标,利用条件![]() ,可得
,可得![]() 点坐标,再代入椭圆方程,可得。
点坐标,再代入椭圆方程,可得。
(2)可先按倾斜角为![]() 是否为直角,分别设过点
是否为直角,分别设过点![]() 直线
直线![]() 方程并与(1)中的椭圆方程联立,通过设出直线与椭圆的交点,再利用
方程并与(1)中的椭圆方程联立,通过设出直线与椭圆的交点,再利用![]() ,建立关于
,建立关于![]() 的关系式,观察可运用均值不等式求出最大值。
的关系式,观察可运用均值不等式求出最大值。
试题解析:(1)设椭圆方程为:![]()
由![]() 得
得![]() ,又知
,又知![]() ,故
,故![]()
从而椭圆方程简化为:![]() .
.
直线![]() ,设
,设![]()
由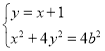 消去
消去![]() 得:
得:![]()
故![]() ①
①
由![]() 知:
知:![]() ②
②
由①②得![]() .易知
.易知![]() ,故
,故![]() ,将其代入椭圆方程
,将其代入椭圆方程![]() 得
得![]()
因此,椭圆方程为:![]()
(2)当![]() 时,直线
时,直线![]() .
.
由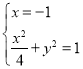 得
得![]() ,
,![]()
故
![]()
当![]() 时,设直线
时,设直线![]() ,
,![]()
由 得
得![]()
![]()

综上可知:当![]() 时,
时,![]() 最大,最大值为
最大,最大值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】本市某玩具生产公司根据市场调查分析,决定调整产品生产方案,准备每天生产![]() ,
, ![]() ,
, ![]() 三种玩具共100个,且
三种玩具共100个,且![]() 种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:
种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:
玩具名称 |
|
|
|
工时(分钟) | 5 | 7 | 4 |
利润(元) | 5 | 6 | 3 |
(Ⅰ)用每天生产![]() 种玩具个数
种玩具个数![]() 与
与![]() 种玩具
种玩具![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(Ⅱ)怎样分配生产任务才能使每天的利润最大,最大利润是多少?