题目内容
(本小题满分12分)
如图,在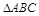 中,设
中,设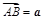 ,
,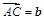 ,
,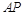 的中点为
的中点为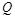 ,
,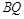 的中点为
的中点为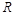 ,
,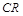 的中点恰为
的中点恰为 .
.
(Ⅰ)若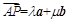 ,求
,求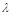 和
和 的值;
的值;
(Ⅱ)以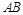 ,
,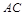 为邻边,
为邻边, 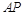 为对角线,作平行四边形
为对角线,作平行四边形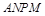 ,
,
求平行四边形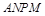 和三角形
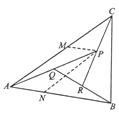
和三角形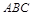 的面积之比
的面积之比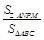 .
.
如图,在
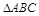 中,设
中,设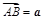 ,
,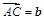 ,
,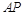 的中点为
的中点为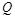 ,
,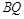 的中点为
的中点为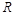 ,
,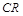 的中点恰为
的中点恰为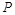 .
.(Ⅰ)若
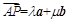 ,求
,求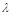 和
和 的值;
的值;(Ⅱ)以
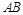 ,
,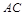 为邻边,
为邻边, 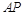 为对角线,作平行四边形
为对角线,作平行四边形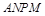 ,
,求平行四边形
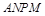 和三角形
和三角形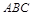 的面积之比
的面积之比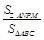 .
.
(1) ;
;
(2)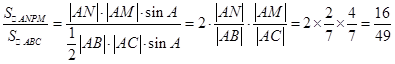
 ;
;(2)
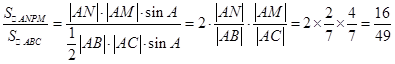
本试题主要是考查了平面向量的基本定理的运用。
(1)∵Q为AP中点,∴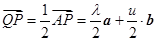 P为CR中点,
P为CR中点,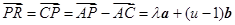 ,
,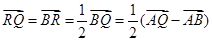 ,得到参数的 值。
,得到参数的 值。
(2)因为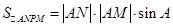
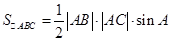
则可结合正弦面积公式得到结论。
(1)解:∵Q为AP中点,∴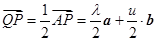 P为CR中点,
P为CR中点,
∴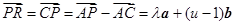
同理: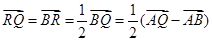
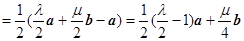
而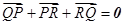 ∴
∴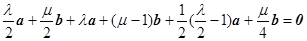
即
(2)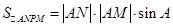
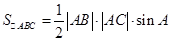
∴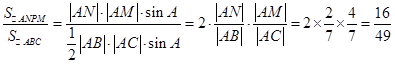
(1)∵Q为AP中点,∴
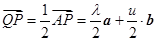 P为CR中点,
P为CR中点,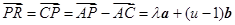 ,
,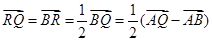 ,得到参数的 值。
,得到参数的 值。(2)因为
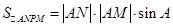
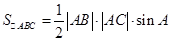
则可结合正弦面积公式得到结论。
(1)解:∵Q为AP中点,∴
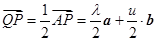 P为CR中点,
P为CR中点,∴
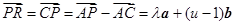
同理:
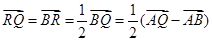
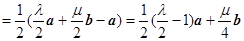
而
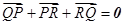 ∴
∴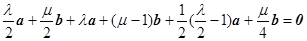
即

(2)
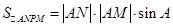
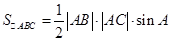
∴
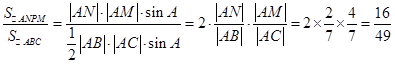

练习册系列答案
相关题目
 时,存在某个位置,使得AB⊥CD
时,存在某个位置,使得AB⊥CD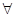 x>0时,都不存在某个位置,使得AB⊥CD
x>0时,都不存在某个位置,使得AB⊥CD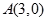 ,
, ,
,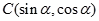 ,其中
,其中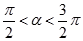 ,
,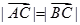 ,求
,求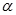 的值
的值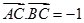 ,求
,求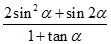 的值
的值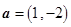 ,
,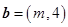 ,且
,且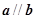 ,那么
,那么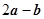 等于( )
等于( )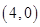
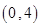
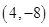
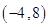
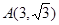 ,O为坐标原点,点P(x,y)的坐标x,y满足
,O为坐标原点,点P(x,y)的坐标x,y满足 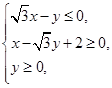
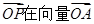 方向上的投影的取值范围是
方向上的投影的取值范围是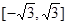
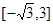
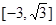
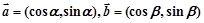 且
且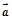 与
与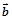 满足关系式:
满足关系式: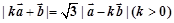 .
.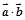 ;
;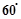 时,求k的值.
时,求k的值.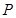 是单位正方体
是单位正方体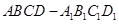 中异于点
中异于点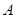 的一个顶点,则
的一个顶点,则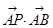 的值为( )
的值为( ) 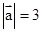 ,
,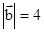 ,且(
,且(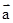 +k
+k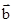 )⊥(
)⊥( k
k 等于
等于



