题目内容
已知:四棱锥P-ABCD的底面ABCD是边长为1的正方形,PD⊥底面ABCD,且PD=1.
(Ⅰ) 求证:BC∥平面PAD;
(Ⅱ)若E、F分别为PB、AD的中点,求证:EF⊥平面PBC;
(Ⅲ)求二面角B-PA-C的余弦值.
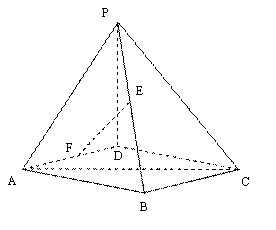
方法1:
(Ⅰ)解:因为ABCD是正方形,
所以BC∥AD.
因为AD![]() 平面PAD,BC
平面PAD,BC![]() 平面PAD,
平面PAD,
所以BC∥平面PAD.
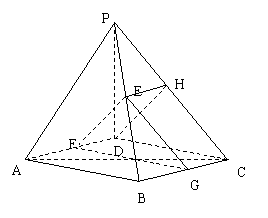 (Ⅱ)
(Ⅱ)
证明:因为PD⊥底面ABCD,
且ABCD是正方形,
所以PC⊥BC.
设BC的中点为G,
连结EG,FG,则EG∥PC,FG∥DC.
所以BC⊥EG,BC⊥FG.
因为 EG∩FG=G,
所以BC⊥面EFG.
因为EF![]() 面EFG,
面EFG,
所以BC⊥EF. ①
又设PC的中点为H,且E为PB中点,
连结DH,
所以EH![]()
![]() BC.
BC.
又BC![]() AD,且EH
AD,且EH![]()
![]() AD.
AD.
所以四边形EHDF是平行四边形.
所以EF∥DH.
因为等腰直角△PDC中,H为底边PC的中点,
所以DH⊥PC,即EF⊥PC. ②
因为PC∩BC=C, ③
由①②③知EF⊥平面PBC.
(②的证明也可以通过连结PF、FB,由△PFB为等腰三角形证明)
(Ⅲ)(理科)
解法1:
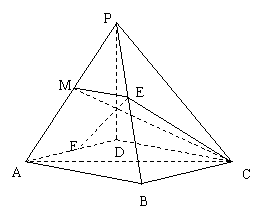 设PA的中点为M,连结MC,
设PA的中点为M,连结MC,
依条件可知△PAC中PC=AC,
所以MC⊥PA. ①
又PD⊥平面ABCD,∠BAD=90°,
所以AB⊥PA.
因为M、E均为中点,
所以ME∥AB.
所以ME⊥PA. ②
由①②知∠EMC为所求二面角的平面角.
连结EC,在△MEC中,容易求出ME=![]() ,MC=
,MC=![]() ,EC=
,EC=![]() .
.
所以cos∠EMC=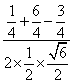 =
=![]() ,即所求二面角的余弦值是
,即所求二面角的余弦值是![]() .
.
解法2:
过点C作CS⊥平面ABCD,使CS=PD.
连结PS,SB,
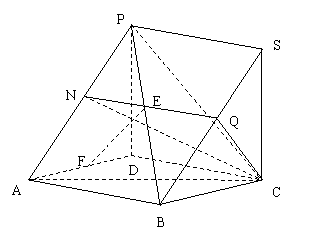 因为PD,AD,DC两两垂直,且四边形
因为PD,AD,DC两两垂直,且四边形
ABCD为正方形,
故容易证明几何体PAD-SBC为三棱柱.
(即以PAD为底面,以DC为高构造三棱柱
PAD-SBC)
设BS的中点为Q,PA中点为N,
连结NQ,NC.
因为ABSP为矩形,N、Q分别为中点,
所以NQ⊥PA.
又△APC中,AC=PC,N为中点,
所以NC⊥PA.
所以∠CNQ为所求二面角的平面角.
因为BC=CS,所以CQ⊥BS.
又面BCS⊥面ABSP,所以CQ⊥面ABSP.
因为NQ![]() 面ABSP,所以CQ⊥NQ.
面ABSP,所以CQ⊥NQ.
在Rt△NCQ中,容易求出NQ=1,NC=![]() ,
,
所以cos∠CNQ=![]() =
=![]() =
=![]() ,即所求二面角的余弦值是
,即所求二面角的余弦值是![]() .
.
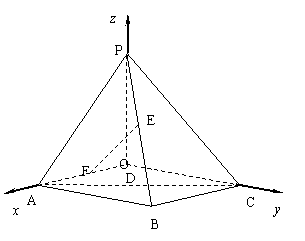 方法2:
方法2:
如图,以点D为原点O,
有向直线OA、OC、OP分别为x、y、z轴
建立空间直角坐标系.
(Ⅰ)证明:因为![]() =(1,0,0),
=(1,0,0),
平面PAD的一个法向量为
rPAD=(0,1,0),
由![]() ? rPAD=0,可得
? rPAD=0,可得![]() ⊥rPAD.
⊥rPAD.
于是BC∥平面PAD.
(Ⅱ)证明:因为![]() =(0,-
=(0,-![]() ,-
,-![]() ),
),![]() =(1,0,0),
=(1,0,0),![]() =(0,-1,1)
=(0,-1,1)
且![]() ?
?![]() =0,
=0,![]() ?
?![]() =0,CB∩CP=C,
=0,CB∩CP=C,
所以EF⊥平面PBC.
(也可以证明![]() 平行于平面PBC的一个法向量)
平行于平面PBC的一个法向量)
(Ⅲ) 解:容易求出平面PAB的一个法向量为rPAB=(![]() ,0,
,0,![]() ),
),
及平面PAC的一个法向量为rPAC=(1,1, 1),
因为rPAB? rPAC=![]() +
+![]() =1,|rPAB|=
=1,|rPAB|=![]() ,|rPAC|=
,|rPAC|=![]() ,
,
所以cos<rPAB, rPAC>=![]() =
=![]() ,即所求二面角的余弦值是
,即所求二面角的余弦值是![]() .
.

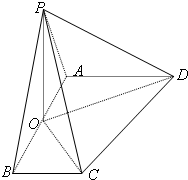 已知在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,O为AB中点,AD∥BC,AB⊥BC,PA=PB=BC=AB=2,AD=3.
已知在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,O为AB中点,AD∥BC,AB⊥BC,PA=PB=BC=AB=2,AD=3. (2013•梅州一模)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB、PD的中点.
(2013•梅州一模)已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB、PD的中点.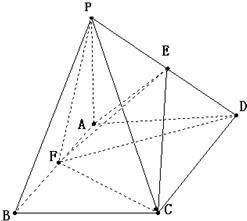 已知:四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,且PA=AB=2,PC与底面ABCD所成角为450,PD的中点为E,F为AB上的动点.
已知:四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,且PA=AB=2,PC与底面ABCD所成角为450,PD的中点为E,F为AB上的动点. (2012•枣庄二模)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
(2012•枣庄二模)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.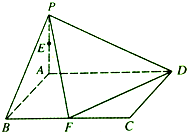 已知在四棱锥P-ABCD,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段PA,BC的中点.
已知在四棱锥P-ABCD,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段PA,BC的中点.