题目内容
下列四个命题;①直线x•cosθ-y+1=0(θ∈R)的倾斜角的取值范围为[
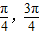 ];
];②直线l1:a1x+b1y+c1=0(a12+b12≠0)与直线l2:a2x+b2y+c2=0(a22+b22≠0),则|
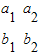 |=0是直线l1、l2平行的必要不充分条件;
|=0是直线l1、l2平行的必要不充分条件;③圆C:x2+y2=r2及点P(x,y),若过点P作圆C的两条切线分别交圆C于A、B两点,则过AB的直线方程为xx+yy=r2;
④方程
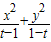 =1不可能表示圆;
=1不可能表示圆;其中正确命题的序号为 .
【答案】分析:①利用直线的斜率和倾斜角的关系判定.②利用行列式的运算和直线平行的等价条件进行判断.③利用直线和圆相切的等价条件进行判断.④利用方程的特点确定方程对应的轨迹方程.
解答:解:①因为直线的标准方程为y=xcosθ+1,所以直线的斜率k=cosθ,所以-1≤k≤1,由-1≤tanα≤1,解得0≤α≤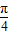 或
或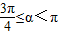 ,所以①错误.
,所以①错误.
②由|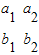 |=0得a1b2-a2b1=0,直线l1、l2平行,则必有a1b2-a2b1=0.若a1b2-a2b1=0时,不妨设c1=c2=0,此时两直线重合,所以|
|=0得a1b2-a2b1=0,直线l1、l2平行,则必有a1b2-a2b1=0.若a1b2-a2b1=0时,不妨设c1=c2=0,此时两直线重合,所以|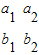 |=0是直线l1、l2平行的必要不充分条件,所以②正确.
|=0是直线l1、l2平行的必要不充分条件,所以②正确.
③由题意可得OP2=x2+y2,所以以OP的中点为圆心,以OP为直径的圆的方程为:(x- )2+(y-
)2+(y- )2=
)2= OP2
OP2
即:(x- )2+(y-
)2+(y- )2=
)2= (x2+y2)…①x2+y2=r2…②,直线AB的方程就是两个圆的公共弦的方程,
(x2+y2)…①x2+y2=r2…②,直线AB的方程就是两个圆的公共弦的方程,
所以①-②得xx+yy=r2,所以③正确.
④若方程表示圆,则有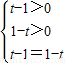 ,即
,即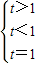 ,不等式组无解,所以方程不可能表示圆,所以④正确.
,不等式组无解,所以方程不可能表示圆,所以④正确.
故答案为:②③④.
点评:本题主要考查各种命题的真假判断,涉及的知识点较多,综合性较强.
解答:解:①因为直线的标准方程为y=xcosθ+1,所以直线的斜率k=cosθ,所以-1≤k≤1,由-1≤tanα≤1,解得0≤α≤
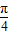 或
或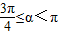 ,所以①错误.
,所以①错误.②由|
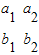 |=0得a1b2-a2b1=0,直线l1、l2平行,则必有a1b2-a2b1=0.若a1b2-a2b1=0时,不妨设c1=c2=0,此时两直线重合,所以|
|=0得a1b2-a2b1=0,直线l1、l2平行,则必有a1b2-a2b1=0.若a1b2-a2b1=0时,不妨设c1=c2=0,此时两直线重合,所以|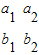 |=0是直线l1、l2平行的必要不充分条件,所以②正确.
|=0是直线l1、l2平行的必要不充分条件,所以②正确.③由题意可得OP2=x2+y2,所以以OP的中点为圆心,以OP为直径的圆的方程为:(x-
 )2+(y-
)2+(y- )2=
)2= OP2
OP2即:(x-
 )2+(y-
)2+(y- )2=
)2= (x2+y2)…①x2+y2=r2…②,直线AB的方程就是两个圆的公共弦的方程,
(x2+y2)…①x2+y2=r2…②,直线AB的方程就是两个圆的公共弦的方程,所以①-②得xx+yy=r2,所以③正确.
④若方程表示圆,则有
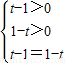 ,即
,即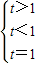 ,不等式组无解,所以方程不可能表示圆,所以④正确.
,不等式组无解,所以方程不可能表示圆,所以④正确.故答案为:②③④.
点评:本题主要考查各种命题的真假判断,涉及的知识点较多,综合性较强.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
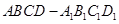 .则下列四个命题
.则下列四个命题
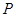 在直线
在直线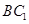 上运动时,三棱锥
上运动时,三棱锥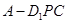 的体积不变;
的体积不变;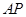 与平面
与平面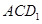 所成的角的大小不变;
所成的角的大小不变;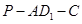 的大小不变;
的大小不变;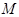 是平面
是平面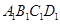 上到点
上到点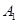 和
和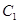 距离相等的点,则
距离相等的点,则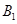
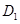 ;
;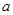 ∥直线
∥直线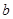 ”的必要不充分条件是“
”的必要不充分条件是“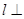 平面
平面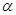 ”的充要条件是“
”的充要条件是“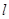 垂直于平面
垂直于平面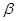 ”是“
”是“