��Ŀ����
�����ĸ����⣻
��ֱ��x•cos��-y+1=0���ȡ�R������б�ǵ�ȡֵ��ΧΪ[
��
]��
��ֱ��l1��a1x+b1y+c1=0��a12+b12��0����ֱ��l2��a2x+b2y+c2=0��a22+b22��0������|
|=0��ֱ��l1��l2ƽ�еı�Ҫ�����������
��ԲC��x2+y2=r2����P��x0��y0����������P��ԲC���������߷ֱ�ԲC��A��B���㣬���AB��ֱ�߷���Ϊxx0+yy0=r2��
�ܷ���
+
=1�����ܱ�ʾԲ��
������ȷ��������Ϊ
��ֱ��x•cos��-y+1=0���ȡ�R������б�ǵ�ȡֵ��ΧΪ[
| �� |
| 4 |
| 3�� |
| 4 |
��ֱ��l1��a1x+b1y+c1=0��a12+b12��0����ֱ��l2��a2x+b2y+c2=0��a22+b22��0������|
|
��ԲC��x2+y2=r2����P��x0��y0����������P��ԲC���������߷ֱ�ԲC��A��B���㣬���AB��ֱ�߷���Ϊxx0+yy0=r2��
�ܷ���
| x2 |
| t-1 |
| y2 |
| 1-t |
������ȷ��������Ϊ
�ڢۢ�
�ڢۢ�
��������������ֱ�ߵ�б�ʺ���б�ǵĹ�ϵ�ж�������������ʽ�������ֱ��ƽ�еĵȼ����������жϣ�������ֱ�ߺ�Բ���еĵȼ����������жϣ������÷��̵��ص�ȷ�����̶�Ӧ�Ĺ켣���̣�
����⣺����Ϊֱ�ߵı�����Ϊy=xcos��+1������ֱ�ߵ�б��k=cos�ȣ�����-1��k��1����-1��tan����1�����0�ܦ���
��
�ܦ����������Ԣٴ���
����|
|=0��a1b2-a2b1=0��ֱ��l1��l2ƽ�У������a1b2-a2b1=0����a1b2-a2b1=0ʱ��������c1=c2=0����ʱ��ֱ���غϣ�����|
|=0��ֱ��l1��l2ƽ�еı�Ҫ��������������Ԣ���ȷ��
��������ɵ�OP2=x02+y02��������OP���е�ΪԲ�ģ���OPΪֱ����Բ�ķ���Ϊ����x-
��2+��y-
��2=
OP2
������x-
��2+��y-
��2=
��x02+y02������x2+y2=r2���ڣ�ֱ��AB�ķ��̾�������Բ�Ĺ����ҵķ��̣�
���Ԣ�-�ڵ�x0x+y0y=r2�����Ԣ���ȷ��
�������̱�ʾԲ������
����
������ʽ���⣬���Է��̲����ܱ�ʾԲ�����Ԣ���ȷ��
�ʴ�Ϊ���ڢۢܣ�
| �� |
| 4 |
| 3�� |
| 4 |
����|
|
|
��������ɵ�OP2=x02+y02��������OP���е�ΪԲ�ģ���OPΪֱ����Բ�ķ���Ϊ����x-
| x0 |
| 2 |
| y0 |
| 2 |
| 1 |
| 4 |
������x-
| x0 |
| 2 |
| y0 |
| 2 |
| 1 |
| 4 |
���Ԣ�-�ڵ�x0x+y0y=r2�����Ԣ���ȷ��
�������̱�ʾԲ������
|
|
�ʴ�Ϊ���ڢۢܣ�
������������Ҫ����������������жϣ��漰��֪ʶ��϶࣬�ۺ��Խ�ǿ��

��ϰ��ϵ�д�
 ����С��ʿ���������ϵ�д�
����С��ʿ���������ϵ�д�
�����Ŀ
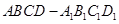 .�������ĸ�����
.�������ĸ�����
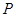 ��ֱ��
��ֱ��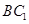 ���˶�ʱ,����
���˶�ʱ,����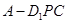 ���������;
���������;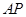 ��ƽ��
��ƽ��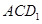 ���ɵĽǵĴ�С���䣻
���ɵĽǵĴ�С���䣻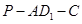 �Ĵ�С���䣻
�Ĵ�С���䣻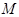 ��ƽ��
��ƽ��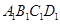 �ϵ���
�ϵ���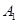 ��
��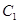 ������ȵĵ㣬��
������ȵĵ㣬��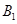
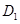 ��
��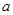 ��ֱ��
��ֱ��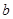 ���ı�Ҫ����������ǡ�
���ı�Ҫ����������ǡ�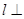 ƽ��
ƽ��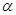 ���ij�Ҫ�����ǡ�
���ij�Ҫ�����ǡ�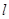 ��ֱ��ƽ��
��ֱ��ƽ��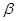 ���ǡ�
���ǡ�