题目内容
3.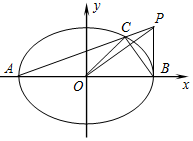 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右顶点分别是A(-$\sqrt{2}$,0),B($\sqrt{2}$,0),离心率为$\frac{{\sqrt{2}}}{2}$.设点P(a,t)(t≠0),连接PA交椭圆于点C,坐标原点是O.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右顶点分别是A(-$\sqrt{2}$,0),B($\sqrt{2}$,0),离心率为$\frac{{\sqrt{2}}}{2}$.设点P(a,t)(t≠0),连接PA交椭圆于点C,坐标原点是O.(Ⅰ)证明:OP⊥BC;
(Ⅱ)若三角形ABC的面积不大于四边形OBPC的面积,求|t|的最小值.
分析 (Ⅰ)由a=$\sqrt{2}$,椭圆的离心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$,求得b,求得椭圆的标准方程,求得直线PA的方程,求得C点坐标,直线BC的斜率kBC=-$\frac{\sqrt{2}}{t}$,直线OP的斜率kBC=$\frac{t}{\sqrt{2}}$,则kBC•kBC=-1,则OP⊥BC;
(Ⅱ)分别求得三角形ABC的面积和四边形OBPC的面积,由题意即可求得|t|的最小值.
解答 解:(Ⅰ)由题意可知:a=$\sqrt{2}$,e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{{\sqrt{2}}}{2}$,则b=1,
∴椭圆的标准方程:$\frac{{x}^{2}}{2}+{y}^{2}=1$,
设直线PA的方程y=$\frac{t}{2\sqrt{2}}$(x+$\sqrt{2}$),
则$\left\{\begin{array}{l}{\frac{{x}^{2}}{2}+{y}^{2}=1}\\{y=\frac{t}{2\sqrt{2}}(x+\sqrt{2})}\end{array}\right.$,
整理得:(4+t2)x2+2$\sqrt{2}$t2x+2t2-8=0,
解得:x1=-$\sqrt{2}$,x2=$\frac{4\sqrt{2}-\sqrt{2}{t}^{2}}{4+{t}^{2}}$,则C点坐标($\frac{4\sqrt{2}-\sqrt{2}{t}^{2}}{4+{t}^{2}}$,$\frac{4t}{4+{t}^{2}}$),
故直线BC的斜率kBC=-$\frac{\sqrt{2}}{t}$,直线OP的斜率kOP=$\frac{t}{\sqrt{2}}$,
∴kBC•kOP=-1,
∴OP⊥BC;
(Ⅱ)由(Ⅰ)可知:四边形OBPC的面积S1=$\frac{1}{2}$×丨OP丨×丨BC丨=$\frac{\sqrt{2}丨{t}^{2}+2t丨}{{t}^{2}+4}$,
则三角形ABC,S2=$\frac{1}{2}$×2$\sqrt{2}$×$\frac{4丨t丨}{4+{t}^{2}}$=$\frac{4\sqrt{2}丨t丨}{{4+t}^{2}}$,
由$\frac{4\sqrt{2}丨t丨}{{4+t}^{2}}$≤$\frac{\sqrt{2}丨{t}^{2}+2t丨}{{t}^{2}+4}$,整理得:t2+2≥4,则丨t丨≥$\sqrt{2}$,
∴丨t丨min=$\sqrt{2}$,
|t|的最小值$\sqrt{2}$.
点评 本题考查椭圆的标准方程及简单几何性质,直线的斜率公式,考查计算能力,属于中档题.

| A. | (x+1)2+(y-1)2=2 | B. | (x+1)2+(y-1)2=4 | C. | (x-1)2+(y+1)2=1 | D. | (x-1)2+(y+1)2=4 |
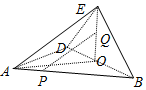 在四边形ABCD中,对角线AC,BD垂直相交于点O,且OA=OB=OD=4,OC=3.
在四边形ABCD中,对角线AC,BD垂直相交于点O,且OA=OB=OD=4,OC=3.



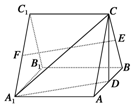 如图,直三棱柱ABC-A1B1C1中,D,E,F分别为棱AB,BC,A1C1的中点.证明:
如图,直三棱柱ABC-A1B1C1中,D,E,F分别为棱AB,BC,A1C1的中点.证明: