题目内容
圆心为（1，1），并与直线3x+4y+3=0相切的圆的方程为________．
（x-1）2+（y-1）2=4．
分析：求出圆心到直线的距离就是圆的半径，然后求出圆的方程即可．
解答：圆心到直线的距离为：r=
=2，
所以所求圆的方程为：（x-1）2+（y-1）2=4．
故答案为：（x-1）2+（y-1）2=4．
点评：本题是基础题，考查圆的方程的求法，注意圆心到直线的距离就是半径，是解题的关键，考查计算能力．
分析：求出圆心到直线的距离就是圆的半径，然后求出圆的方程即可．
解答：圆心到直线的距离为：r=
=2，所以所求圆的方程为：（x-1）2+（y-1）2=4．
故答案为：（x-1）2+（y-1）2=4．
点评：本题是基础题，考查圆的方程的求法，注意圆心到直线的距离就是半径，是解题的关键，考查计算能力．
练习册系列答案
全优测试卷系列答案
冲刺100分1号卷系列答案
相关题目
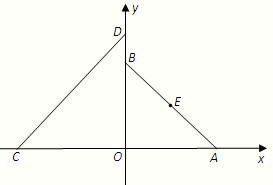如图，在平面直角坐标系xOy中，A（a，0）（a＞0），B（0，a），C（-4，0），D（0，4），设△AOB的外接圆圆心为E．