题目内容
已知函数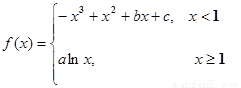 的图像过坐标原点
的图像过坐标原点 ,且在点
,且在点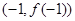 处的切线的斜率是
处的切线的斜率是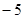 .
.
(1)求实数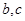 的值;
的值;
(2)求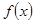 在区间
在区间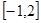 上的最大值;
上的最大值;
(3)对任意给定的正实数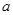 ,曲线
,曲线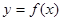 上是否存在两点
上是否存在两点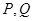 ,使得
,使得 是以
是以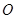 为
为
直角顶点的直角三角形,且此三角形斜边的中点在轴上?请说明理由.
【答案】
(I) . (II)
. (II)
 对任意给定的正实数
对任意给定的正实数 ,曲线
,曲线 上总存在两点
上总存在两点 ,使得
,使得 是以
是以 为直角顶点的直角三角形,且此三角形斜边的中点在y轴上.
(12分)
为直角顶点的直角三角形,且此三角形斜边的中点在y轴上.
(12分)
【解析】本试题主要是考查导数在研究函数中的运用。
(1)当x<1时,由f(x)=-x3+x2+bx+c,知f′(x)=-3x2+2x+b.依题意f′(-1)=-5,故b=0,再由f(0)=0,能求出c=0.
(2)当x<1时,由f(x)=-x3+x2,知f′(x)=-3x2+2x,令f′(x)=0,得x=0,x=
.列表讨论,得f(-1)=2;f(0)=0;f( )=
)= ;f(1)=0.由此进行分类讨论,能求出f(x)在区间[-1,2]上的最大值.
;f(1)=0.由此进行分类讨论,能求出f(x)在区间[-1,2]上的最大值.
(3)不妨设 ,则
,则 ,显然
,显然
因为 是以
是以 为直角顶点的直角三角形,
为直角顶点的直角三角形,
所以 ,即
,即 结合方程有解来分析求解。
结合方程有解来分析求解。

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目

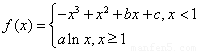
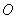

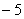
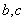

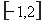
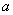
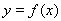

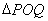
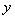














 的图像过坐标原点
的图像过坐标原点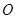 ,且在点
,且在点 处的切线
处的切线 .
. 的值; (2)求
的值; (2)求 在区间
在区间 上的最大值;
上的最大值;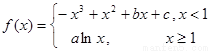 的图像过坐标原点
的图像过坐标原点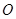 ,且在点
,且在点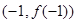 处的切线的斜率是
处的切线的斜率是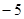 .
.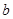 ,
,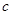 的值
的值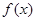 在区间
在区间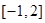 上的值域
上的值域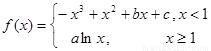 的图像过坐标原点
的图像过坐标原点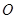 ,且在点
,且在点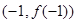 处的切线的斜率是
处的切线的斜率是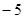 .
.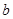 ,
,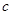 的值
的值 在区间
在区间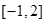 上的值域
上的值域