题目内容
(满分12分)设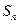 为数列
为数列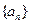 的前
的前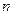 项和,对任意的
项和,对任意的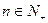 ,都有
,都有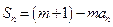
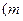 为常数,且
为常数,且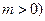 .
.
(1)求证:数列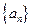 是等比数列;
是等比数列;
(2)设数列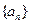 的公比
的公比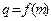 ,数列
,数列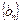 满足
满足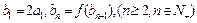 ,求数列
,求数列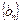 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列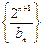 的前
的前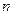 项和
项和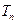 .
.
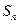 为数列
为数列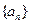 的前
的前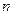 项和,对任意的
项和,对任意的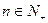 ,都有
,都有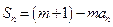
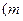 为常数,且
为常数,且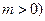 .
.(1)求证:数列
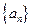 是等比数列;
是等比数列;(2)设数列
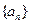 的公比
的公比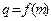 ,数列
,数列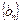 满足
满足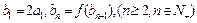 ,求数列
,求数列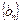 的通项公式;
的通项公式;(3)在满足(2)的条件下,求数列
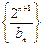 的前
的前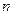 项和
项和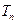 .
.(1)证明:当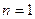 时,
时,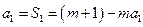 ,解得
,解得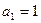 .
.
当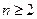 时,
时,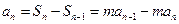 .即
.即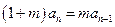 .
.
又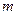 为常数,且
为常数,且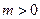 ,∴
,∴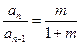
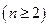 .
.

∴数列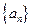 是首项为1,公比为
是首项为1,公比为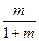 的等比数列.
的等比数列.
(2)解:由(1)得,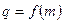
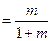 ,
,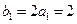 .
.
∵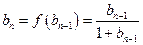 ,∴
,∴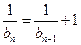 ,即
,即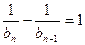
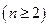 .
.
∴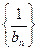 是首项为
是首项为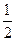 ,
, 公差为1的等差数列.
公差为1的等差数列.
∴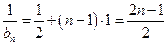 ,即
,即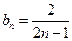 (
(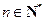 ).
).
(3)解:由(2)知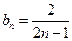 ,则
,则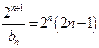 .
.
所以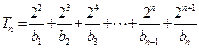 ,…8分
,…8分
即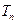
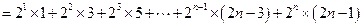 , ①
, ①
则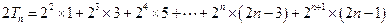 , ②
, ②
②-①得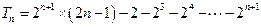 ,
,
故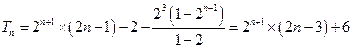
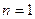 时,
时,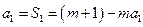 ,解得
,解得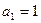 .
.当
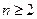 时,
时,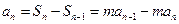 .即
.即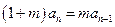 .
. 又
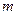 为常数,且
为常数,且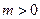 ,∴
,∴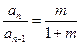
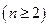 .
.
∴数列
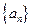 是首项为1,公比为
是首项为1,公比为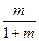 的等比数列.
的等比数列.(2)解:由(1)得,
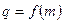
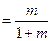 ,
,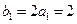 .
. ∵
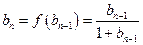 ,∴
,∴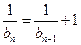 ,即
,即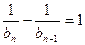
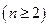 .
. ∴
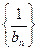 是首项为
是首项为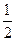 ,
, 公差为1的等差数列.
公差为1的等差数列.∴
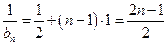 ,即
,即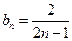 (
(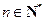 ).
).(3)解:由(2)知
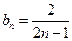 ,则
,则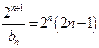 .
.所以
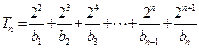 ,…8分
,…8分即
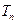
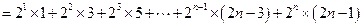 , ①
, ① 则
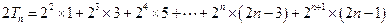 , ②
, ②②-①得
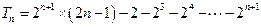 ,
,故
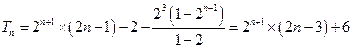
略

练习册系列答案
相关题目
 中,
中,
 ,
, ,则使前
,则使前 项和
项和 成立的最大自然数
成立的最大自然数







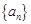 .若
.若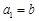 (
(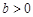 ),
),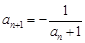 (
(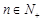 ),则能使
),则能使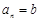 成立
成立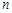 的值可能是
的值可能是 n项和为Sn,且a3=5,S15="225."
n项和为Sn,且a3=5,S15="225." 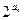 +2n,求数列{bn}的前n项和Tn.
+2n,求数列{bn}的前n项和Tn.  中,已知
中,已知 ,那么
,那么 =( )
=( )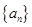 中,若
中,若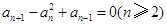 ,
,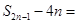 ( )
( )



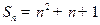 , 则数列的通项an=
, 则数列的通项an=