题目内容
设△ABC的三内角为A、B、C,且满足4cos2
-cos2(B+C)=
(Ⅰ)求角A的大小;(Ⅱ)当|x|≤A时,求函数f(x)=
sinxcosx+
sin2x的值域.
| A |
| 2 |
| 7 |
| 2 |
(Ⅰ)求角A的大小;(Ⅱ)当|x|≤A时,求函数f(x)=
| 1 |
| 2 |
| ||
| 2 |
(Ⅰ)△ABC中,∵A+B+C=π,∴4cos2
-cos2(B+C)=2+2cosA-cos2A
=-2cos2A+2cosA+3=
,∴cosA=
,∵0<A<π,∴A=
.
(Ⅱ) 当x∈[-
,
]时,函数f(x)=
sinxcosx+
sin2x=
+
sin2x-
cos2x
=
+
sin(-
+2x),由-π≤2x-
≤
,可得-1≤sin(-
+2x)≤
,
∴
≤f(x)≤
,即函数的值域为[
,
].
| A |
| 2 |
=-2cos2A+2cosA+3=
| 7 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
(Ⅱ) 当x∈[-
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| 1 |
| 4 |
| ||
| 4 |
=
| ||
| 4 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
∴
| ||
| 4 |
| ||
| 2 |
| ||
| 4 |
| ||
| 2 |

练习册系列答案
相关题目
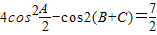
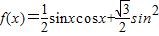 x的值域.
x的值域. 、
、 ,
,
 ,则C等于( )
,则C等于( )  B.
B. C.
C. D.
D.
 、
、 ,
,
 ,则C等于( )
,则C等于( ) B、
B、 C、
C、 D、
D、