Question

设△ABC的三内角为A、B、C，且满足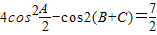
（Ⅰ）求角A的大小；（Ⅱ）当|x|≤A时，求函数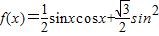x的值域．

Answer 1

【答案】分析：（Ⅰ）利用三角形内角和把cos2（B+C）转化成cos2A，把题设等式转化成关于cosA的一元二次方程求得cosA，进而根据A的范围求得A．
（Ⅱ） 根据x的范围求出角2x-的范围，利用两角差的正弦公式化简函数解析式为  + sin（-+2x），
求出sin（-+2x）的范围，可得函数的值域．
解答：解：（Ⅰ）△ABC中，∵A+B+C=π，∴=2+2cosA-cos2A 
=-2cos²A+2cosA+3=，∴cosA=，∵0＜A＜π，∴A=．
（Ⅱ） 当x∈[-，]时，函数x=+sin2x-
=+ sin（-+2x），由-π≤2x-≤，可得-1≤sin（-+2x）≤，
∴≤f（x）≤，即函数的值域为[，]．
点评：本题主要考查二倍角公式，两角差的正弦公式的应用，根据x的范围求出角2x-的范围以及sin（-+2x）的范围，
是解题的难点．