Question

已知点A（-1，0），B（0，2），当平移抛物线y²=x并使它的顶点在线段AB上运动时，抛物线截直线y=x的线段长的最大值是（　　）

• A．

  34

• B．

  10

• C．

  3 2

  2

• D．3

  2

Answer 1

分析：先根据直线的两点式方程求出直线方程，然后根据题意设出抛物线的顶点坐标，表示出抛物线方程，然后与直线y=x联立方程组，从而表示出抛物线截直线y=x的线段长，从而求出最值．

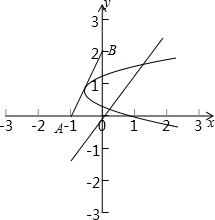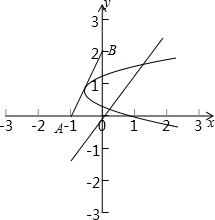解答：解：线段AB的方程为：

x-(-1)

0-(-1)

=

y-0

2-0

即y=2（x+1），
当平移抛物线y²=x并使它的顶点在线段AB上运动时：顶点坐标设为（k，2（k+1））
∴抛物线方程为：[y-2（k+1）]²=x-k
它与y=x联立方程组

[y-2(k+1)]2=x-k y=x

，
得：[x-2（k+1）]²=x-k，
即x²-（4k+5）x+4（k+1）²+k=0，
两交点设为（x₁，y₁）、（x₂，y₂），
根据韦达定理：x₁+x₂=4k+5，x₁x₂=4（k+1）²+k，
∴抛物线截直线y=x的线段长为：

(x2-x1)2+(y2-y1)2

=

1+1

•

(x2-x1)2

=

2

•

(x1+x2)2-4x1x2

=

8k+18

，
∴抛物线截直线y=x的线段长的最大值发生在B点，最大值为3

2

．
故选D．

点评：本题主要考查了抛物线的应用，以及弦长公式l=

(x2-x1)2+(y2-y1)2

=

1+k2

•

(x2-x1)2

的应用，同时考查了分析问题的能力和运算求解的能力，属于中档题．