题目内容
(本题满分15分)设函数![]() 且
且![]() 是奇函数,(1)求
是奇函数,(1)求![]() 的值;(2)若
的值;(2)若![]() ,试求不等式
,试求不等式![]() 的解集;(3)若
的解集;(3)若![]() ,且
,且![]() 在
在![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的值.
的值.
(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]() 或
或![]()
![]() (Ⅲ)
(Ⅲ)![]()
解析:
(1)∵ ![]() 为奇函数, ∴
为奇函数, ∴ ![]() , ∴
, ∴ ![]() , ∴
, ∴ ![]() ……3分
……3分
(2)∵ ![]() , ∴
, ∴ ![]() , ∴
, ∴ ![]() ,……5分
,……5分
又![]() ∴
∴ ![]() 在R上单调递增…7分
在R上单调递增…7分
原不等式可化为: ![]() ,∴
,∴ ![]() ,即
,即![]() ,
,
∴ ![]() 或
或![]() ,∴ 不等式的解集为
,∴ 不等式的解集为![]() 或
或![]()
![]() …9分
…9分
(3)∵ ![]() , ∴
, ∴ ![]() ,即
,即![]() , ∴
, ∴ ![]() 或
或![]() (舍去)…11分
(舍去)…11分
∴ ![]()
令![]() , ∵
, ∵ ![]() , ∴
, ∴ ![]() ,
,
∴ ![]() ,……13分
,……13分
当![]() 时,当
时,当![]() 时,
时,![]() , ∴
, ∴ ![]() ,当
,当![]() 时,当
时,当![]() 时,
时,![]() ,
,![]() ,舍去, ∴
,舍去, ∴ ![]() . …15分
. …15分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
. 在
在 上单调递增,在
上单调递增,在 上单调递减,求实数
上单调递减,求实数 的最大值;
的最大值; 对任意的
对任意的 ,
, 都成立,求实数
都成立,求实数 的取值范围.
的取值范围. 为自然对数的底数.
为自然对数的底数.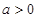 ,函数
,函数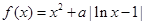 .
. 时,求函数
时,求函数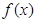 的单调增区间;
的单调增区间; 时,不等式
时,不等式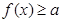 恒成立,实数
恒成立,实数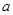 的取值范围.
的取值范围.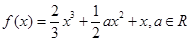 .
.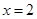 时,
时,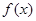 取得极值,求
取得极值,求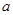 的值;
的值;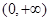 内为增函数,求
内为增函数,求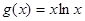 ,是否存在正实数
,是否存在正实数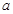 ,使得对任意
,使得对任意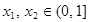 ,都有
,都有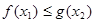 成立?
成立?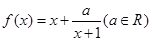 .
.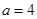 时,解不等式:
时,解不等式: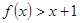 ;
;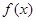 在
在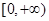 的最小值;
的最小值;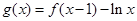 的单调递增区间.
的单调递增区间.