题目内容
在平面直角坐标系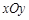 中,动点
中,动点 到两点
到两点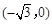 ,
,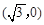 的距离之和等于4,设点
的距离之和等于4,设点 的轨迹为曲线C,直线过点
的轨迹为曲线C,直线过点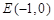 且与曲线C交于A,B两点.
且与曲线C交于A,B两点.
(Ⅰ)求曲线C的轨迹方程;
(Ⅱ)是否存在△AOB面积的最大值,若存在,求出△AOB的面积;若不存在,请说明理由.
(Ⅰ) ;(Ⅱ)存在;最大值为
;(Ⅱ)存在;最大值为
解析试题分析:该题考察曲线方程的求法、直线和椭圆的位置关系、函数的最大值,考察数形结合、综合分析问题和解决问题的能力.(Ⅰ)由已知曲线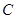 是以
是以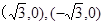 为焦点的椭圆,且
为焦点的椭圆,且 ,故曲线
,故曲线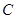 的方程为
的方程为 ;(Ⅱ)设过点
;(Ⅱ)设过点 的直线方程为:
的直线方程为: ,将它与椭圆:
,将它与椭圆: 联立,可得
联立,可得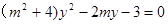 ,设
,设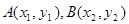 ,
,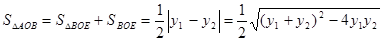 ,然后根据韦达定理代入,可得关于
,然后根据韦达定理代入,可得关于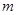 的函数,再求其最大值即可.
的函数,再求其最大值即可.
试题解析:(Ⅰ)由椭圆定义可知,点 的轨迹C是以
的轨迹C是以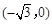 ,
,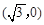 为焦点,长半轴长为2的椭圆.
为焦点,长半轴长为2的椭圆.
故曲线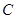 的方程为
的方程为 . 4分
. 4分
(Ⅱ)存在△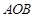 面积的最大值.
面积的最大值.
因为直线过点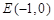 ,可设直线的方程为
,可设直线的方程为  或
或 (舍).
(舍).
则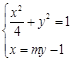
整理得  . 7分
. 7分
由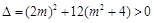 .
.
设 .
.
解得 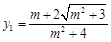 ,
,  .
.
则  .
.
因为
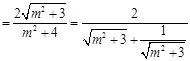 . 10分
. 10分
设 ,
, ,
,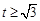 .
.
则 在区间
在区间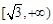 上为增函数.
上为增函数.
所以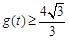 .
.
所以 ,当且仅当
,当且仅当 时取等号,即
时取等号,即 .
.
所以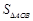 的最大值为
的最大值为 . 12分
. 12分
考点:1、曲线的方程的求法;2、直线和椭圆的位置关系;3、函数的最大值.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 的中心在坐标原点,边
的中心在坐标原点,边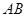 与
与 轴平行,
轴平行, =6.
=6.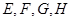 分别是矩形四条边的中点,
分别是矩形四条边的中点,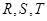 是线段
是线段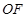 的四等分点,
的四等分点,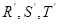 是线段
是线段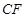 的四等分点.设直线
的四等分点.设直线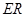 与
与 ,
, 与
与 ,
, 与
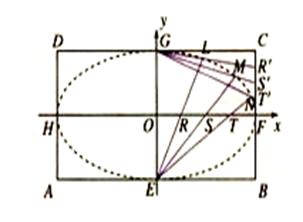
与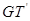 的交点依次为
的交点依次为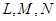 .
.
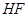 为长轴,以
为长轴,以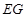 为短轴的椭圆Q的方程;
为短轴的椭圆Q的方程;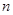 (
(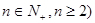 等分点从左向右依次为
等分点从左向右依次为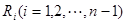 ,线段
,线段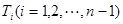 ,那么直线
,那么直线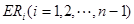 与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)
与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)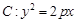 的焦点坐标为
的焦点坐标为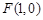 ,过
,过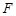 的直线交抛物线
的直线交抛物线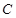 于
于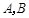 两点,直线
两点,直线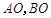 分别与直线
分别与直线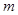 :
: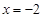 相交于
相交于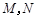 两点.
两点.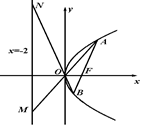
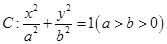 过点
过点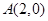 ,离心率为
,离心率为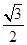 .
.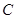 的方程;
的方程;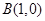 且斜率为
且斜率为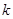 (
(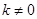 )的直线
)的直线 与椭圆
与椭圆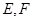 两点,直线
两点,直线 、
、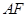 分别交直线
分别交直线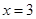 于
于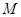 、
、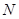 两点,线段
两点,线段 的中点为
的中点为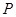 .记直线
.记直线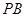 的斜率为
的斜率为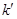 ,求证:
,求证: 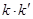 为定值.
为定值. :
:
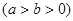 ,
,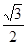 ,求椭圆的标准方程;
,求椭圆的标准方程;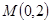 的直线
的直线 与椭圆
与椭圆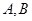 ,且
,且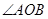 为锐角(
为锐角( 为坐标原点),求直线
为坐标原点),求直线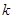 的取值范围;
的取值范围;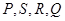 四点,设原点
四点,设原点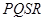 的一边距离为
的一边距离为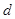 ,试求
,试求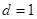 时
时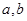 满足的条件.
满足的条件.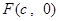 是椭圆
是椭圆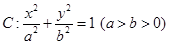 的右焦点,圆
的右焦点,圆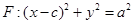 与
与 轴交于
轴交于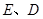 两点,
两点,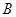 是椭圆
是椭圆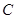 与圆
与圆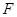 的一个交点,且
的一个交点,且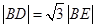
 与
与 ,且
,且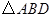 的面积为
的面积为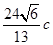 ,求椭圆
,求椭圆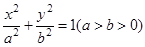 的离心率为
的离心率为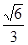 ,且过点
,且过点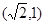 .
.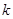 的直线
的直线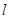 与椭圆相交于不同的两点
与椭圆相交于不同的两点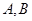 ,试问在
,试问在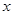 轴上是否存在点
轴上是否存在点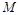 ,使
,使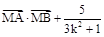 是与
是与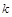 无关的常数?若存在,求出点
无关的常数?若存在,求出点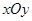 中,已知曲线
中,已知曲线 上任意一点到点
上任意一点到点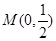 的距离与到直线
的距离与到直线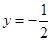 的距离相等.
的距离相等.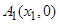 ,
,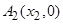 是
是 轴上的两点
轴上的两点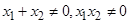 ,过点
,过点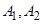 分别作
分别作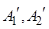 ,直线
,直线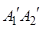 与x轴交于点
与x轴交于点 ,这样就称
,这样就称 确定了
确定了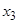 .同样,可由
.同样,可由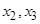 确定了
确定了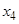 .现已知
.现已知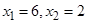 ,求
,求