Question

函数y=a^4-x（a＞0，a≠1）的图象恒过定点A，若点A在直线mx+ny-1=0（mn＞0）上，则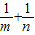的最小值为    ．

Answer 1

【答案】分析：利用a=1（a≠0）即可得出定点A，代入直线mx+ny-1=0（mn＞0）即可得到m、n的关系，再利用“乘1法”和基本不等式即可得出．
解答：解：x=4时，y=a^4-4=a=1，∴函数y=a^4-x（a＞0，a≠1）的图象恒过定点A（4，1），代入直线mx+ny-1=0（mn＞0）得4m+n=1，
∴==5+≥=9，当且仅当n=2m=是取等号．
故答案为9．
点评：熟练掌握a=1（a≠0）、“乘1法”和基本不等式是解题的关键．