题目内容
已知椭圆C的长轴长与短轴长之比为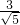 ,焦点坐标分别为F1(-2,0),F2(2,0).
,焦点坐标分别为F1(-2,0),F2(2,0).
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知A(-3,0),B(3,0),P是椭圆C上异于A、B的任意一点,直线AP、BP分别交y轴于M、N,求 的值.
的值.
解:(Ⅰ) 设椭圆C的标准方程为 .
.
∵ ,c=2,a2=b2+c2
,c=2,a2=b2+c2
∴a2=9,b2=5…(4分)
所以椭圆C的标准方程为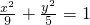 .…(5分)
.…(5分)
(Ⅱ)设P(x0,y0),直线 ,
,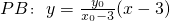 …(7分)
…(7分)
令x=0,得: ,
, …(9分)
…(9分)
∵P点在椭圆上,∴
所以: ,…(12分)
,…(12分)
分析:(Ⅰ) 设椭圆C的标准方程为 ,利用椭圆C的长轴长与短轴长之比为
,利用椭圆C的长轴长与短轴长之比为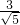 ,焦点坐标分别为F1(-2,0),F2(2,0),确定几何量之间的关系,从而可求椭圆C的标准方程;
,焦点坐标分别为F1(-2,0),F2(2,0),确定几何量之间的关系,从而可求椭圆C的标准方程;
(Ⅱ)设P(x0,y0),可得直线方程,令x=0,从而可求M,N的坐标,根据P点在椭圆上,即可求得 的值.
的值.
点评:本题考查椭圆的标准方程,考查直线方程,求椭圆的标准方程,利用待定系数法是我们常用的方法.
 .
.∵
 ,c=2,a2=b2+c2
,c=2,a2=b2+c2∴a2=9,b2=5…(4分)
所以椭圆C的标准方程为
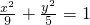 .…(5分)
.…(5分)(Ⅱ)设P(x0,y0),直线
 ,
,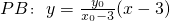 …(7分)
…(7分)令x=0,得:
 ,
, …(9分)
…(9分)∵P点在椭圆上,∴

所以:
 ,…(12分)
,…(12分)分析:(Ⅰ) 设椭圆C的标准方程为
 ,利用椭圆C的长轴长与短轴长之比为
,利用椭圆C的长轴长与短轴长之比为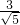 ,焦点坐标分别为F1(-2,0),F2(2,0),确定几何量之间的关系,从而可求椭圆C的标准方程;
,焦点坐标分别为F1(-2,0),F2(2,0),确定几何量之间的关系,从而可求椭圆C的标准方程;(Ⅱ)设P(x0,y0),可得直线方程,令x=0,从而可求M,N的坐标,根据P点在椭圆上,即可求得
 的值.
的值.点评:本题考查椭圆的标准方程,考查直线方程,求椭圆的标准方程,利用待定系数法是我们常用的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
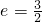 的双曲线的标准方程.
的双曲线的标准方程.