题目内容
已知椭圆C的长轴长与短轴长之比为| 3 | ||
|
(1)求椭圆C的方程;
(2)已知A(-3,0),B(3,0),p(xp,yp)是椭圆C在第一象限部分上的一动点,且∠APB是钝角,求xp的取值范围;
分析:(1)根据题意可知c的值,进而根据
=
和a2=b2+c2求得b,椭圆的方程可得.
(2)先用xp和yp表示出
和
进而根据∠APB是钝角判断
•
<0,进而根据椭圆方程求得xp的范围,又根据点p在第一象限进而可得答案.
| a |
| b |
| 3 | ||
|
(2)先用xp和yp表示出
| PA |
| PB |
| PA |
| PB |
解答:解:(1)∵
=
,c=2,a2=b2+c2
∴a2=9,b2=5
所以椭圆C的标准方程为
+
=1.
(2)∵
=(-3-xp,-yp),
=(3-xp,-yp)
且∠APB是钝角
∴
•
=xp2-9+yp2<0
又∵
+
=1
∴-3<xp<3
又∵点p在第一象限
所以:0<xp<3
| a |
| b |
| 3 | ||
|
∴a2=9,b2=5
所以椭圆C的标准方程为
| x2 |
| 9 |
| y2 |
| 5 |
(2)∵
| PA |
| PB |
且∠APB是钝角
∴
| PA |
| PB |
又∵
| xp2 |
| 9 |
| yp2 |
| 5 |
∴-3<xp<3
又∵点p在第一象限
所以:0<xp<3
点评:本题主要考查了椭圆的标准方程和向量的基本知识.考查了学生逻辑思维能力和综合分析问题的能力.

练习册系列答案
相关题目
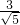 ,焦点坐标分别为F1(-2,0),F2(2,0).
,焦点坐标分别为F1(-2,0),F2(2,0).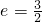 的双曲线的标准方程.
的双曲线的标准方程.