题目内容
如图所示,在矩形ABCD中,AB=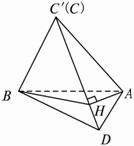
(1)求证:BC′⊥平面AC′D;?
(2)求点A到平面BC′D的距离;?
(3)求直线AB与平面BC′D所成角的大小.
(1)证明:∵点C′在平面ABC上的射影O在AB上,∴C′O⊥?平面ABD,故斜线BC′在平面ABD上的射影为AB.∵DA⊥AB,∴DA⊥BC′(三垂线定理).?
又∵BC⊥CD,∴BC′⊥C′D.?
∵DA∩C′D=D,∴BC′⊥平面AC′D.?
(2)解析:如图所示,过A作AH⊥C′D于H,∵BC′⊥平面AC′D,∴BC′⊥AH.?
∴AH⊥平面BC′D.故AH的长就是A点到平面BC′D的距离.?
∵DA⊥AB,DA⊥BC,∴DA⊥平面ABC′.∴DA⊥AC′.?

在Rt△AC′B中,?
AC′=![]() ,?
,?
在Rt△BC′D中,C′D=CD=![]() .?
.?
在Rt△C′AD中,由面积关系,得AH=![]() ,即点A到平面BC′D的距离.?
,即点A到平面BC′D的距离.?
另法:(等积代换法)点A到平面BC′D的距离看成以A为顶点,以△BC′D为底面的三棱锥的高,利用等积代换思想有VA—BC′D =VC′—ABD?.设点A到平面BC′D的距离为d,又?C′D?⊥面ABD,?
∴C′O是三棱锥C′—ABD的高.?
∴![]() S△BC′D?·d=
S△BC′D?·d=![]() S△ABD?·C′O.?
S△ABD?·C′O.?
∴d=![]() .?
.?
由平面图形和立体图形知BC′⊥C′D,??
∴C′B=BC=3,C′D=AB=![]() .?
.?
∴BD=![]() =6.?
=6.?
∴S△BC′D?=![]() ×3×3
×3×3![]() .?
.?
又∵DA⊥AB于A,?
∴DA=3,AB=3![]() .?
.?
∴S△ABD?=![]() ×3×3
×3×3![]() .?
.?
又由(1)知C′B⊥平面AC′D,?
∴C′B⊥C′A.?
又AB=3![]() ,C′B=3,∴C′A=
,C′B=3,∴C′A=![]() .?
.?
∴C′O=![]() .?
.?
∴d=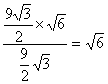 .?
.?
∴点A到平面BC′D的距离为![]() .?
.?
(3)解析:连结BH,?
∵AH⊥平面BC′D,?
∴BH是AB在平面BC′D上的射影.故∠ABH就是直线AB与平面BC′D所成的角.?
在Rt△AHB中,sin∠AHB=![]() .?
.?
∴∠AHB=arcsin![]() .?
.?
∴直线AB与平面BC′D所成角的大小为arcsin![]() .
.

 名校课堂系列答案
名校课堂系列答案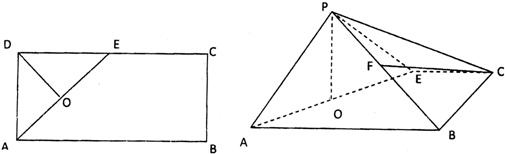 19、如图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且PC=PB,F是BP的中点.
19、如图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且PC=PB,F是BP的中点.
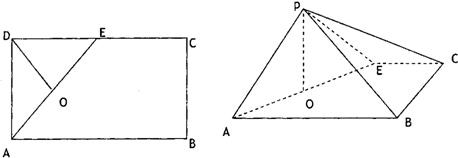
 如图所示,在矩形ABCD中,AB=4cm,BC=2cm,在图形上随机撒一粒黄豆,则黄豆落到圆上的概率是
如图所示,在矩形ABCD中,AB=4cm,BC=2cm,在图形上随机撒一粒黄豆,则黄豆落到圆上的概率是 如图所示,在矩形ABCD中,已知AB=a,BC=b.a≤3b,在AB,AD,CD,CB上分别截取AE,AH,CG,CF,且都等于x,则四边形EFGH面积的最大值为
如图所示,在矩形ABCD中,已知AB=a,BC=b.a≤3b,在AB,AD,CD,CB上分别截取AE,AH,CG,CF,且都等于x,则四边形EFGH面积的最大值为