题目内容
【题目】已知函数
．
（1） 求函数
的单调递减区间；
（2） 当
时，的最小值是
，求实数
的值．
【答案】（1） 
时，
的单调递减区间为
，
时，
的单调递减区间为
．（2） 
【解析】
试题分析：（1） 先求函数导数，再根据导函数在定义域上零点情况讨论：时，无零点，函数单调减；时，有一个零点，减区间为．（2）先根据导函数在定义域上是否变号进行讨论：
时，导函数不变号，函数单调减；
时，导函数不变号，函数单调增；
时，导函数变号，先减后增，再根据对应最小值取法，列等量关系，进而确定实数
的值．
试题解析：（1） 
时，
在上恒成立，
则的单调递减区间为，
时，令得：
，
则的单调递减区间为．
①
时，在
上单调递减，
，无解
②时， 在上单调递增，
，
解得：
，适合题意；
③时，在
上单调递减，
上单调递增，
，解得：
，舍去；
综上：．
练习册系列答案
相关题目
【题目】为贯彻落实教育部等
部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,普及足球知识和技能,市教体局决定举行春季校园足球联赛,为迎接此次联赛,甲中学选拔了
名学生组成集训队,现统计了这名学生的身高,记录如下表：
身高 |
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
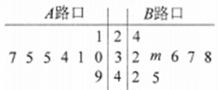
（1）请计算这名学生的身高中位数、众数,并补充完成下面的茎叶图：
（2）身高为
和
的四名学生分别为
,现从这四名学生中选
名担任正副门将,请利用列举法列出所有可能情况,并求学生
入选正门将的概率．
