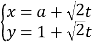Question

【题目】己知两点，，动点P在y轴上的摄影是H，且，

（1）求动点P的轨迹方程；

（2）设直线，的两个斜率存在，分别记为，，若，求点P的坐标；

（3）若经过点的直线l与动点P的轨迹有两个交点为T、Q，当时，求直线l的方程.

Answer 1

【答案】（1）

（2）点或P或或

（3）

【解析】

(1)设，则，表示出，，的坐标，代入后化简，即可求出所求;

(2)由(1)可知点坐标设为，由两点间的斜率公式求得，，并代入化简，再与(1)所得的轨迹方程联立，即可求解出点坐标；

(3)设出，，再设出直线的方程的点斜式，让其与动点的轨迹方程联立化简得一个含斜率的一元二次方程，由韦达定理写出根与系数的关系，结合两点间的距离公式化简，进而求出直线的斜率，得到直线的方程.

（1）设，则，又，，

∵，∴所以动点P的轨迹方程为

（2）由题意得：，，所以，即

又由（1）可得，所以解得，

即点或P或或

（3）设直线方程，联立方程组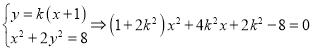

计算恒成立

设，，所以，

所以

即，解得

直线l的方程为