题目内容
6.设a1,a2,…an,…为一实数数列,且对所有的正整数n满足an+1=$\frac{n(n+1)}{2}$-an请问下列哪些选项是正确的?
(1)如果a1=1,则a2=1
(2)如果a1是正整数,则此数列的每一项都是整数
(3)如果a1是无理数,则此数列的每一项都是无理数
(4)a2≤a4≤…≤a2n≤…(n为正整数)
(5)如果ak是奇数,则ak+2,ak+4,…,ak+2n,…都是奇数(n为正整数)
分析 利用递推公式对五个逐个进行判断,由此能求出结果.
解答 解:由a1,a2,…an,…为一实数数列,且对所有的正整数n满足an+1=$\frac{n(n+1)}{2}$-an,知:
在(1)中:若a1=1,则${a}_{2}=\frac{1×2}{2}-1$=0,故(1)错误,
在(2)中:若a1是整数,且对所有正整数n,$\frac{n(n+1)}{2}$必为整数,
∴${a}_{2}=\frac{n(n+1)}{2}-{a}_{1}$为整数,${a}_{n+1}=\frac{n(n+1)}{2}-{a}_{n}$为整数,故(2)正确;
在(3)中:若a1是无理数,则${a}_{2}=\frac{1×2}{2}-{a}_{1}=1-{a}_{1}$是无理数,
∴${a}_{n+1}=\frac{n(n+1)}{2}-{a}_{n}$是无理数,故(3)正确;
在(4)中:${a}_{n+2}=\frac{(n+1)(n+2)}{2}-{a}_{n+1}$=$\frac{(n+1)(n+2)}{2}-$($\frac{n(n+1)}{2}-{a}_{n}$)=an+(n+1),
∴an+2>an,∴a2≤a4≤…≤a2n≤…(n为正整数),故(4)正确;
在(5)中:∵ak+2=ak+(k+1),∴a3=a1+2,a5=a3+4,a7=a5+6,…
且a4=a2+3,a6=a4+5,a8=a6+7,…
∴若a1是奇数,则a3,a5,…都是奇数,∴a2n+1都是奇数,
若a2是奇数,则a4是偶数,a6是奇数,…,∴a2n+2奇偶相间,故(5)错误.
综上:(1)、(5)错误,(2)、(3)、(4)正确.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意递推公式的合理运用.

| A. | (9,8) | B. | (-7,-4) | C. | (7,4) | D. | (-9,-8) |
| A. | 都是偶函数 | |
| B. | 一个奇函数,一个偶函数,两个非奇非偶函数 | |
| C. | 一个奇函数,两个偶函数,一个非奇非偶函数 | |
| D. | 一个奇函数,三个偶函数 |
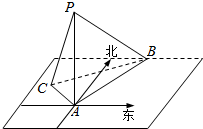 如图所示,在海岛A上有一座海拔$\sqrt{3}$千米的山峰上,山顶上设有一座观察站P,一艘轮船沿一固定方向匀速航行,上午10:00时,测得此船在岛北偏东20°且俯角为30°的B处,到10:10时,又测得该船在岛北偏西40°且俯角为60°的C处,则该船的航行速度为$6\sqrt{7}$千米/时.
如图所示,在海岛A上有一座海拔$\sqrt{3}$千米的山峰上,山顶上设有一座观察站P,一艘轮船沿一固定方向匀速航行,上午10:00时,测得此船在岛北偏东20°且俯角为30°的B处,到10:10时,又测得该船在岛北偏西40°且俯角为60°的C处,则该船的航行速度为$6\sqrt{7}$千米/时.