题目内容
A是正方形BCDE所成平面外一点,AE⊥平面BCDE,且AE=CD=a,G、H分别是BE、ED的中点,则GH到平面ABD的距离是( )A.
a B.
a C.
a D.
a
答案:D
解析:设BD的中点为R,连结AR、ER,则BD⊥ER,BD⊥AE,∴BD⊥平面AER,平面ABD⊥平面AER,交线是AR;再过ER与GH的交点作AR的垂线段,即为所求.
练习册系列答案
应用题作业本系列答案
相关题目
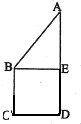（2012•安庆二模）如图正方形BCDE的边长为a，已知AB=
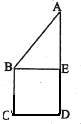如图正方形BCDE的边长为a，已知AB=
BC，将直角△ABE沿BE边折起，A点在面BCDE上的射影为D点，则翻折后的几何体中有如下描述：
；
；
．
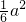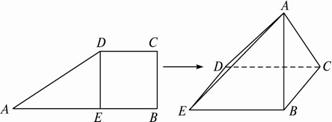
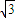BC，将直角△ABE沿BE边折起，A点在面BCDE上的射影为D点，则翻折后的几何体中有如下描述：
；
；
．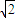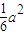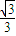